题目内容
11.在进行二次根式运算时,我们有时会碰上如$\frac{5}{{\sqrt{3}}}$、$\frac{2}{{\sqrt{3}+1}}$这样的式子,其实我们还可以将其进一步化简:$\frac{5}{{\sqrt{3}}}=\frac{{5×\sqrt{3}}}{{\sqrt{3}×\sqrt{3}}}=\frac{5}{3}\sqrt{3}$;$\frac{2}{{\sqrt{3}+1}}=\frac{{2×(\sqrt{3}-1)}}{{(\sqrt{3}+1)(\sqrt{3}-1)}}=\frac{{2(\sqrt{3}-1)}}{{{{(\sqrt{3})}^2}-1}}=\sqrt{3}-1$.以上这种化简过程叫做分母有理化.$\frac{2}{{\sqrt{3}+1}}$还可以用以下方法化简:$\frac{2}{{\sqrt{3}+1}}=\frac{3-1}{{\sqrt{3}+1}}=\frac{{{{(\sqrt{3})}^2}-{1^2}}}{{\sqrt{3}+1}}=\frac{{(\sqrt{3}+1)(\sqrt{3}-1)}}{{\sqrt{3}+1}}=\sqrt{3}-1$
试用上述方法化简下列各式:
(1)$\frac{1}{{\sqrt{7}+\sqrt{6}}}$;
(2)$\frac{2}{{\sqrt{3}+1}}+\frac{2}{{\sqrt{5}+\sqrt{3}}}+\frac{2}{{\sqrt{7}+\sqrt{5}}}+…+\frac{2}{{\sqrt{99}+\sqrt{97}}}$.
分析 (1)把分子分母都乘以$\sqrt{7}$-$\sqrt{6}$,然后利用平方差公式计算即可;
(2)先把每个二次根式进行分母有理化,然后合并即可.
解答 解:(1)原式=$\frac{{1×(\sqrt{7}-\sqrt{6})}}{{(\sqrt{7}+\sqrt{6})(\sqrt{7}-\sqrt{6})}}$
=$\frac{{\sqrt{7}-\sqrt{6}}}{{{{(\sqrt{7})}^2}-{{(\sqrt{6})}^2}}}$
=$\sqrt{7}-\sqrt{6}$;
(2)原式=$(\sqrt{3}-1)+(\sqrt{5}-\sqrt{3})+(\sqrt{7}-\sqrt{5})$+…+$(\sqrt{99}-\sqrt{97})$
=$\sqrt{99}-1$
=$3\sqrt{11}-1$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.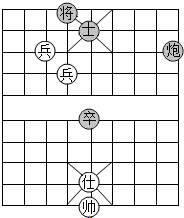 如图是中国象棋的一盘残局,如果用(8,7)表示“炮”的位置,用(3,9)表示“将”的位置,那么“帅”的位置应该表示为( )
如图是中国象棋的一盘残局,如果用(8,7)表示“炮”的位置,用(3,9)表示“将”的位置,那么“帅”的位置应该表示为( )
 如图是中国象棋的一盘残局,如果用(8,7)表示“炮”的位置,用(3,9)表示“将”的位置,那么“帅”的位置应该表示为( )
如图是中国象棋的一盘残局,如果用(8,7)表示“炮”的位置,用(3,9)表示“将”的位置,那么“帅”的位置应该表示为( )| A. | (8,7) | B. | (0,4) | C. | (0,0) | D. | (4,0) |
3. 如图,矩形ABCD的周长是28,对角线AC,BD相交于点O,点E是CD的中点,AC=10,则△DOE的周长是( )
如图,矩形ABCD的周长是28,对角线AC,BD相交于点O,点E是CD的中点,AC=10,则△DOE的周长是( )
 如图,矩形ABCD的周长是28,对角线AC,BD相交于点O,点E是CD的中点,AC=10,则△DOE的周长是( )
如图,矩形ABCD的周长是28,对角线AC,BD相交于点O,点E是CD的中点,AC=10,则△DOE的周长是( )| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
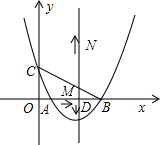 △ABC在平面直角坐标系中的位置,如图所示,点A的坐标为(1,0),点C的坐标为(0,3),关于x的二次函数y=x2+bx+c的图象过点A、B、C,抛物线的对称轴与x轴交于点D.
△ABC在平面直角坐标系中的位置,如图所示,点A的坐标为(1,0),点C的坐标为(0,3),关于x的二次函数y=x2+bx+c的图象过点A、B、C,抛物线的对称轴与x轴交于点D.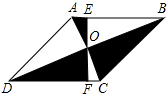 如图,在?ABCD中,对角线AC,BD相交于点O,过O作直线交AD于点E,交BC于点F.若?ABCD的面积为30,则阴影部分的面积是15.
如图,在?ABCD中,对角线AC,BD相交于点O,过O作直线交AD于点E,交BC于点F.若?ABCD的面积为30,则阴影部分的面积是15.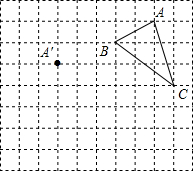 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为A′,点B′、C′分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为A′,点B′、C′分别是B、C的对应点. 如图,已知AF∥CD,AB∥DE,那么∠A=∠D吗?请说明理由.
如图,已知AF∥CD,AB∥DE,那么∠A=∠D吗?请说明理由.