题目内容
10.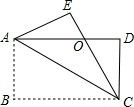 如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.
如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.(1)求证:AO=CO;
(2)若∠OCD=30°,AB=$\sqrt{3}$,求△AOC的面积.
分析 (1)由矩形的性质和折叠的性质证明∠DAC=∠ECA,即可得到AO=CO;
(2)首先求出AO,CO的长,再由三角形面积公式计算即可.
解答 (1)证明:
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAC=∠BCA,
又由折叠可知:∠BCA=∠ECA,
∴∠DAC=∠ECA,
∴OA=OC;
(2)在Rt△COD中,∠D=90°∠OCD=30°
∴OD=$\frac{1}{2}$OC,
又∵AB=CD=$\sqrt{3}$,
∴($\frac{1}{2}$OC)2=OC2-($\sqrt{3}$)2,
∴OC=2,
∴AO=OC=2,
∴S△AOC=$\frac{1}{2}$AO•CD=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$
点评 本题考查了矩形的性质以及翻折变换的性质,熟记矩形的各种性质以及三角形的面积公式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.计算(-3a-bc)•(bc-3a)的结果等于( )
| A. | bc2-9a2 | B. | b2c2-3a2 | C. | 9a2-b2c2 | D. | b2c2-9a2 |
19.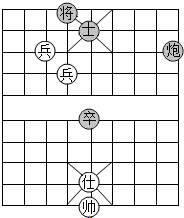 如图是中国象棋的一盘残局,如果用(8,7)表示“炮”的位置,用(3,9)表示“将”的位置,那么“帅”的位置应该表示为( )
如图是中国象棋的一盘残局,如果用(8,7)表示“炮”的位置,用(3,9)表示“将”的位置,那么“帅”的位置应该表示为( )
 如图是中国象棋的一盘残局,如果用(8,7)表示“炮”的位置,用(3,9)表示“将”的位置,那么“帅”的位置应该表示为( )
如图是中国象棋的一盘残局,如果用(8,7)表示“炮”的位置,用(3,9)表示“将”的位置,那么“帅”的位置应该表示为( )| A. | (8,7) | B. | (0,4) | C. | (0,0) | D. | (4,0) |
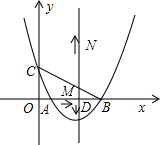 △ABC在平面直角坐标系中的位置,如图所示,点A的坐标为(1,0),点C的坐标为(0,3),关于x的二次函数y=x2+bx+c的图象过点A、B、C,抛物线的对称轴与x轴交于点D.
△ABC在平面直角坐标系中的位置,如图所示,点A的坐标为(1,0),点C的坐标为(0,3),关于x的二次函数y=x2+bx+c的图象过点A、B、C,抛物线的对称轴与x轴交于点D.
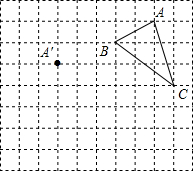 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为A′,点B′、C′分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为A′,点B′、C′分别是B、C的对应点.