题目内容
15．若$\sqrt{{a}^{3}+{a}^{2}}$=-a$\sqrt{a+1}$，那么实数a的取值范围是（ ）| A． | a≥-1 | B． | a≤1 | C． | 0＜a≤1 | D． | -1≤a≤0 |
分析 直接利用二次根式的性质化简得出a的取值范围．
解答 解：∵$\sqrt{{a}^{3}+{a}^{2}}$=-a$\sqrt{a+1}$，
∴-a≥0，且a+1≥0，
解得：-1≤a≤0．
故选：D．
点评 此题主要考查了二次根式的性质与化简，正确掌握二次根式的性质是解题关键．
练习册系列答案
出彩同步大试卷系列答案
相关题目
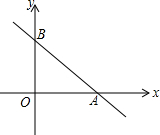如图，一次函数y=-x+1的图象与x轴、y轴分别交于点A、B，点M在x轴上，要使△ABM是以AB为腰的等腰三角形，那么点M的坐标是（$\sqrt{2}$+1，0）、（-$\sqrt{2}$+1，0）或（-1，0）．
