题目内容
20.在函数y=$\frac{2}{x+4}$中,自变量x的取值范围是x≠-4.分析 根据分母不等于0列式计算即可得解.
解答 解:根据题意得,x+4≠0,
解得x≠-4.
故答案为x≠-4.
点评 本题考查了函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
5.不等式组$\left\{\begin{array}{l}x>-1\\ 2x-1<0\end{array}\right.$的解集是( )
| A. | x>-1 | B. | x<$\frac{1}{2}$ | C. | -1<x<$\frac{1}{2}$ | D. | x>$\frac{1}{2}$ |
15.若$\sqrt{{a}^{3}+{a}^{2}}$=-a$\sqrt{a+1}$,那么实数a的取值范围是( )
| A. | a≥-1 | B. | a≤1 | C. | 0<a≤1 | D. | -1≤a≤0 |
 将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是60°.
将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是60°.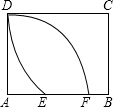 如图所示,以矩形的顶点A为圆心AD的长为半径画圆交AB于点F,再以C为圆心CD的长为半径画圆,交AB于点E,若AD=5,CD=$\frac{17}{3}$,则EF的长是2.
如图所示,以矩形的顶点A为圆心AD的长为半径画圆交AB于点F,再以C为圆心CD的长为半径画圆,交AB于点E,若AD=5,CD=$\frac{17}{3}$,则EF的长是2.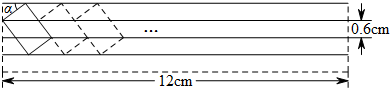
 如图,在△ABC中,AB=AC,点B在直线DE上,若AC∥DE,∠CBE=36°,则∠ABD的度数是108°.
如图,在△ABC中,AB=AC,点B在直线DE上,若AC∥DE,∠CBE=36°,则∠ABD的度数是108°.