题目内容
4．已知关于x的方程x2-2x+3k=0有两个不相等的实数根，则k的取值范围是（ ）| A． | k＜$\frac{1}{3}$ | B． | k＞$-\frac{1}{3}$ | C． | k＜$\frac{1}{3}$且k≠0 | D． | k＞$-\frac{1}{3}$且k≠0 |
分析 根据方程有两个不相等的实数根，得到根的判别式大于0，即可求出k的范围．
解答 解：∵方程x2-2x+3k=0有两个不相等的实数根，
∴△=4-12k＞0，
解得：k＜$\frac{1}{3}$．
故选A．
点评 此题考查了根的判别式，熟练掌握根的判别式的意义是解本题的关键．
练习册系列答案
相关题目
14．
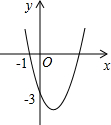如图，抛物线y=ax2+bx+c（a≠0）过点（-1，0）和点（0，-3），且顶点在第四象限，设P=a+b+c，则P的取值范围是（ ）
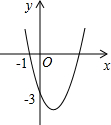如图，抛物线y=ax2+bx+c（a≠0）过点（-1，0）和点（0，-3），且顶点在第四象限，设P=a+b+c，则P的取值范围是（ ）| A． | -3＜P＜-1 | B． | -6＜P＜0 | C． | -3＜P＜0 | D． | -6＜P＜-3 |
15．某校九年级（1）班全体学生2015年初中毕业体育考试的成绩统计如下表：
根据上表中的信息判断，下列结论中错误的是（ ）
| 成绩（分） | 35 | 39 | 42 | 44 | 45 | 48 | 50 |
| 人数（人） | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
| A． | 该班一共有40名同学 | |
| B． | 该班学生这次考试成绩的众数是45分 | |
| C． | 该班学生这次考试成绩的中位数是45分 | |
| D． | 该班学生这次考试成绩的平均数是45分 |
如图，在正方形ABCD中，如果AF=BE，那么∠AOD的度数是90°．
如图，在Rt△ABC中，∠ACB=90°，E是BC的中点，以AC为直径的⊙O与AB边交于点D，连接DE
16．九（1）班组织班级联欢会，最后进入抽奖环节，每名同学都有一次抽奖机会，抽奖方案如下：将一副扑克牌中点数为“2”，“3”，“3”，“5”，“6”的五张牌背面朝上洗匀，先从中抽出1张牌，再从余下的4张牌中抽出1张牌，记录两张牌点数后放回，完成一次抽奖，记每次抽出两张牌点数之差为x，按表格要求确定奖项．
（1）用列表或画树状图的方法求出甲同学获得一等奖的概率；
（2）是否每次抽奖都会获奖，为什么？
| 奖项 | 一等奖 | 二等奖 | 三等奖 |
| |x| | |x|=4 | |x|=3 | 1≤|x|＜3 |
（2）是否每次抽奖都会获奖，为什么？
小敏上午8：00从家里出发，骑车去一家超市购物，然后从这家超市返回家中．小敏离家的路程y（米）和所经过的时间x（分）之间的函数图象如图所示．请根据图象回答下列问题：