题目内容
16．九（1）班组织班级联欢会，最后进入抽奖环节，每名同学都有一次抽奖机会，抽奖方案如下：将一副扑克牌中点数为“2”，“3”，“3”，“5”，“6”的五张牌背面朝上洗匀，先从中抽出1张牌，再从余下的4张牌中抽出1张牌，记录两张牌点数后放回，完成一次抽奖，记每次抽出两张牌点数之差为x，按表格要求确定奖项．| 奖项 | 一等奖 | 二等奖 | 三等奖 |
| |x| | |x|=4 | |x|=3 | 1≤|x|＜3 |
（2）是否每次抽奖都会获奖，为什么？
分析 （1）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与甲同学获得一等奖的情况，再利用概率公式即可求得答案；
（2）由树状图可得：当两张牌都是3时，|x|=0，不会有奖．
解答 解：（1）画树状图得：
∵共有20种等可能的结果，甲同学获得一等奖的有2种情况，
∴甲同学获得一等奖的概率为：$\frac{2}{20}$=$\frac{1}{10}$；
（2）不一定，当两张牌都是3时，|x|=0，不会有奖．
点评 此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
6．
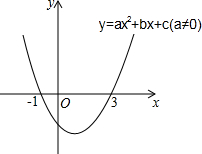二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法：
①2a+b=0
②当-1≤x≤3时，y＜0
③若（x1，y1）、（x2，y2）在函数图象上，当x1＜x2时，y1＜y2
④9a+3b+c=0
其中正确的是（ ）
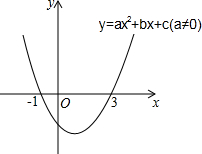二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法：①2a+b=0
②当-1≤x≤3时，y＜0
③若（x1，y1）、（x2，y2）在函数图象上，当x1＜x2时，y1＜y2
④9a+3b+c=0
其中正确的是（ ）
| A． | ①②④ | B． | ①④ | C． | ①②③ | D． | ③④ |
7．下列各点中，在函数y=-$\frac{8}{x}$图象上的是（ ）
| A． | （-2，4） | B． | （2，4） | C． | （-2，-4） | D． | （8，1） |
4．已知关于x的方程x2-2x+3k=0有两个不相等的实数根，则k的取值范围是（ ）
| A． | k＜$\frac{1}{3}$ | B． | k＞$-\frac{1}{3}$ | C． | k＜$\frac{1}{3}$且k≠0 | D． | k＞$-\frac{1}{3}$且k≠0 |
1．据中国电子商务研究中心监测数据显示，2015年第一季度中国轻纺城市场群的商品成交额达27 800 000 000元，将27 800 000 000用科学记数法表示为（ ）
| A． | 2.78×1010 | B． | 2.78×1011 | C． | 27.8×1010 | D． | 0.278×1011 |
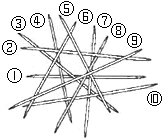挑游戏棒是一种好玩的游戏，游戏规则：当一根棒条没有被其它棒条压着时，就可以把它往上拿走．如图中，按照这一规则，第1次应拿走⑨号棒，第2次应拿走⑤号棒，…，则第6次应拿走（ ）
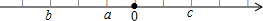如图，a，b，c在数轴上的位置，求代数式$\sqrt{{a}^{2}}$-|a-b|+$\sqrt{{a}^{2}-2ac+{c}^{2}}$．