题目内容
14.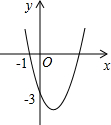 如图,抛物线y=ax2+bx+c(a≠0)过点(-1,0)和点(0,-3),且顶点在第四象限,设P=a+b+c,则P的取值范围是( )
如图,抛物线y=ax2+bx+c(a≠0)过点(-1,0)和点(0,-3),且顶点在第四象限,设P=a+b+c,则P的取值范围是( )| A. | -3<P<-1 | B. | -6<P<0 | C. | -3<P<0 | D. | -6<P<-3 |
分析 利用二次函数图象的开口方向和对称轴求出a>0,b<0,把x=-1代入求出b=a-3,把x=1代入得出P=a+b+c=2a-6,求出2a-6的范围即可.
解答 解:∵抛物线y=ax2+bx+c(c≠0)过点(-1,0)和点(0,-3),
∴0=a-b+c,-3=c,
∴b=a-3,
∵当x=1时,y=ax2+bx+c=a+b+c,
∴P=a+b+c=a+a-3-3=2a-6,
∵顶点在第四象限,a>0,
∴b=a-3<0,
∴a<3,
∴0<a<3,
∴-6<2a-6<0,
即-6<P<0.
故选:B.
点评 此题主要考查了二次函数图象的性质,根据图象过(-1,0)和点(0,-3)得出a与b的关系,以及当x=1时a+b+c=P是解决问题的关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
4. 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )
 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
5.计算:1-(-$\frac{1}{3}$)=( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
6.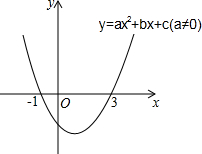 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:
①2a+b=0
②当-1≤x≤3时,y<0
③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2
④9a+3b+c=0
其中正确的是( )
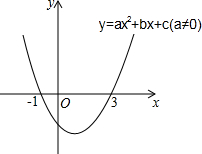 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0
②当-1≤x≤3时,y<0
③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2
④9a+3b+c=0
其中正确的是( )
| A. | ①②④ | B. | ①④ | C. | ①②③ | D. | ③④ |
4.已知关于x的方程x2-2x+3k=0有两个不相等的实数根,则k的取值范围是( )
| A. | k<$\frac{1}{3}$ | B. | k>$-\frac{1}{3}$ | C. | k<$\frac{1}{3}$且k≠0 | D. | k>$-\frac{1}{3}$且k≠0 |
 如图,?ABCD中,点E,F在对角线BD上,且BE=DF,求证:
如图,?ABCD中,点E,F在对角线BD上,且BE=DF,求证: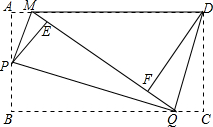 如图,矩形纸片ABCD,将△AMP和△BPQ分别沿PM和PQ折叠(AP>AM),点A和点B都与点E重合;再将△CQD沿DQ折叠,点C落在线段EQ上点F处.
如图,矩形纸片ABCD,将△AMP和△BPQ分别沿PM和PQ折叠(AP>AM),点A和点B都与点E重合;再将△CQD沿DQ折叠,点C落在线段EQ上点F处.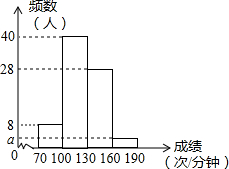 “阳光体育”运动关乎每个学生未来的幸福生活,今年五月,我市某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛,要求每个班选2-3名选手参赛,现将80名选手比赛成绩(单位:次/分钟)进行统计.绘制成频数分布直方图,如图所示.
“阳光体育”运动关乎每个学生未来的幸福生活,今年五月,我市某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛,要求每个班选2-3名选手参赛,现将80名选手比赛成绩(单位:次/分钟)进行统计.绘制成频数分布直方图,如图所示.