题目内容
1．方程x2+4x-$\frac{10}{x}$+1=0的正数根的取值范围是（ ）| A． | 0＜x＜1 | B． | 1＜x＜2 | C． | 2＜x＜3 | D． | 3＜x＜4 |
分析 结合方程的特点，可将方程的正数解看成函数y1=x2+4x+1与函数y2=$\frac{10}{x}$（x＞0）的交点，画出两函数的图象，代入x=1、x=2结合函数的连贯性即可得出结论．
解答 解：方程x2+4x-$\frac{10}{x}$+1=0的正数根可看成函数y1=x2+4x+1与函数y2=$\frac{10}{x}$（x＞0）的交点．
画出两函数的图象，如图所示．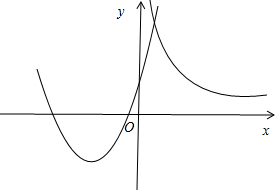
当x=1时，y1=12+4×1+1=6，y2=$\frac{10}{1}$=10，
∴此时函数y2=$\frac{10}{x}$的图象在函数y1=x2+4x+1的上方；
当x=2时，y1=22+4×2+1=13，y2=$\frac{10}{2}$=5，
∴此时函数y2=$\frac{10}{x}$的图象在函数y1=x2+4x+1的下方．
∴函数y1=x2+4x+1与函数y2=$\frac{10}{x}$（x＞0）的交点的横坐标1＜x＜2．
故选B．
点评 本题考查了二次函数的图象以及反比例函数的图象，解题的关键是代入x=1、x=2确定交点的范围．本题属于基础题，难度不大，解决该题型题目时，根据方程的构成特点，将方程的解看成两函数图象的交点问题是关键．
练习册系列答案
相关题目
11．某商品的进货成本为每件200元，促销期间，这种商品按原售价的8折出售，此时每卖出一件这种商品，只能获得10%的利润，设这种商品的原来售价是x元，所列方程正确的是（ ）
| A． | $\frac{0.8x-200}{200}$×100%=10% | B． | $\frac{200-0.8x}{200}$×100%=10% | ||
| C． | $\frac{0.8x-200}{x}$×100%=10% | D． | $\frac{200-0.8x}{x}$×100%=10% |
9．若正比例函数y=2x的图象经过点A（m，3m+1），则m的值为（ ）
| A． | 1 | B． | -1 | C． | $\frac{2}{5}$ | D． | -$\frac{2}{5}$ |
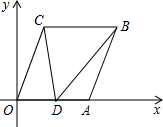如图，在直角坐标系xOy中，已知A（6，0），B（8，6），将线段OA平移至CB，点D在x轴正半轴上（不与点A重合），连接OC，AB，CD，BD．
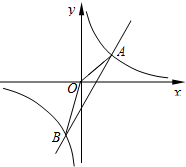如图，已知反比例函数y1=$\frac{{k}_{1}}{x}$的图象与一次函数y2=k2x+b的图象交于A、B两点，A（2，n），B（-$\frac{1}{2}$，-2）．