题目内容
11.如图,点A(a,0),B(0,6)分别在x轴、y轴上,且$\sqrt{\frac{a}{4}}$=$\sqrt{2}$.(1)求线段AB的长;
(2)若点C在线段AB上,D,E分别在线段OA,OB上,且AD=AC,BE=BC.
①如图1,若C为AB的中点,连接CD,CE,试判断△CDE的形状并说明理由;
②如图2,过点D作DF⊥CD交CE的延长线于点F,若点F(m,-m),请求出此时点C的坐标.

分析 (1)由$\sqrt{\frac{a}{4}}$=$\sqrt{2}$.求出a=8,由勾股可求得AB即可解答;
(2)①△CDE为等腰直角三角形;如图1,过点C作CG⊥OA于G,证明△EOD≌△DGC(SAS),得到ED=DC,∠EDO=∠DCG,又∠DCG+∠CDG=90°,∠EDO+∠CDG=90°,所以△CDE为等腰直角三角形;
②首先证明△CDF为等腰直角三角形,过点F作FM⊥x轴于点M,过点C作CN⊥x轴于点N,连接OF,证明△FMD≌△DNC(AAS),得到FM=DN,DM=CN,再证明FM=OM,ON=CN,再根据S△AOB=$\frac{1}{2}$OA×OB=$\frac{1}{2}$OA×CN+$\frac{1}{2}$OB×ON=24,解得ON=$\frac{24}{7}$,即可解答.
解答 解:(1)由$\sqrt{\frac{a}{4}}$=$\sqrt{2}$.
∴a=8,
∴点A(8,0),B(0,6)
由勾股可求得AB=$\sqrt{A{O}^{2}+B{O}^{2}}=\sqrt{{8}^{2}+{6}^{2}}$;
(2)①如图1,过点C作CG⊥OA于G,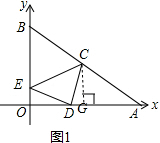
∵C为AB的中点,AD=AC,BE=BC.
∴AD=AC=BE=BC=5,
∴OE=1,CG=3,DG=1,OD=3,
即OE=DG,OD=CG,又∠CGD=∠EOD=90°,
∴△EOD≌△DGC(SAS),
∴ED=DC,∠EDO=∠DCG,
又∠DCG+∠CDG=90°,
∴∠EDO+∠CDG=90°,
∴△CDE为等腰直角三角形;
②∵AD=AC,BE=BC,
∴∠BCE=∠BEC,∠ACD=∠ADC,
又∠ABO+∠BAO=90°,
∴∠FCD=45°,
又∵DF⊥CD,
∴△CDF为等腰直角三角形,
如图②过点F作FM⊥x轴于点M,过点C作CN⊥x轴于点N,连接OF,OC,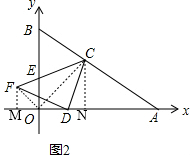
易证△FMD≌△DNC(AAS)
∴FM=DN,DM=CN,
∵F(m,-m),
∴FM=OM,
易证ON=CN,
S△AOB=$\frac{1}{2}$OA×OB=$\frac{1}{2}$OA×CN+$\frac{1}{2}$OB×ON=24,
即$\frac{1}{2}$(OA+OB)×ON=24,
解得ON=$\frac{24}{7}$,
∴C($\frac{24}{7}$,$\frac{24}{7}$).
点评 本题考查了等腰直角三角形的性质定理与判定定理,解决本题的关键是作出辅助线,构建全等三角形.

| A. | 0<x<1 | B. | 1<x<2 | C. | 2<x<3 | D. | 3<x<4 |
| A. | -x2+y2 | B. | 4a2-(a+b)2 | C. | a2-8b2 | D. | x2y2-1 |
| A. | x+2y=3z | B. | xy=1 | C. | x+y=1 | D. | x-yz=2008 |
| A. | 25 | B. | 16 | C. | 9 | D. | 4 |
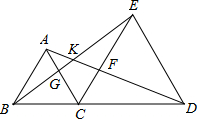 如图,C是线段BD上一点,分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形对数有( )
如图,C是线段BD上一点,分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形对数有( )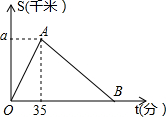 2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途经紫金大桥,沿比赛路线跑回终点万地广场西门.设该运动员离开起点的路程S(千米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,根据图象提供的信息,解答下列问题:
2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途经紫金大桥,沿比赛路线跑回终点万地广场西门.设该运动员离开起点的路程S(千米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,根据图象提供的信息,解答下列问题: