题目内容
8．
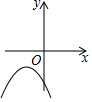如图，一次函数y=x与二次函数y=ax2+bx+c图象相交于A、B两点，则函数y=ax2+（b-1）x+c的图象可能是（ ）| A． |  | B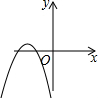． |  | C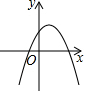． |  | D． |  |
分析 由直线y=x与抛物线y=ax2+bx+c有两个交点，且两交点的横坐标均为负数可知：方程ax2+bx+c=x，即ax2+（b-1）x+c=0有两个同为异号的实数根，根据二次函数的图象与一元二次方程的根之间的关系即可得．
解答 解：由图象知直线y=x与抛物线y=ax2+bx+c有两个交点，且两交点的横坐标均为负数，
∴方程ax2+bx+c=x，即ax2+（b-1）x+c=0有两个同为异号的实数根，
∴函数y=ax2+（b-1）x+c的图象与x轴的负半轴有两个交点，
故选：B．
点评 本题主要考查二次函数的图象与一元二次方程的根之间的关系，由题目已知图象得出方程ax2+bx+c=x，即ax2+（b-1）x+c=0有两个同为异号的实数根是解题的关键．
练习册系列答案
相关题目
已知，△ABC在平面直角坐标系中的位置如图所示．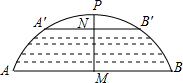
如图所示，有一座拱桥圆弧形，它的跨度AB为60米，拱高PM为18米，当洪水泛滥到跨度只有30米时，就要采取紧急措施，若拱顶离水面只有4米，即PN=4米时，是否采取紧急措施？（$\sqrt{2}$=1.414）
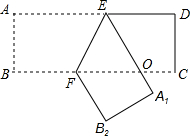如图，把一张长方形纸片ABCD沿EF折叠后，点A、B分别落在A1、B2的位置上，A1E与BC交于点O，若∠EFO=60°，则∠AEA1=120°．
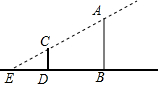小芳的房间有高为3m的玻璃窗，她站在室内离窗户4m的地方向外看，她能看到窗前面一楼房的高度范围是18m（楼房之间的距离为20m）
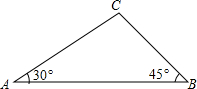如图，在△ABC中，∠A=30°，∠B=45°，AC=2$\sqrt{3}$，则CB的长为$\sqrt{6}$．
4．某公司2007年的利润是a万元，计划以后每年在前一年的基础上增长m%，则2010年的利润是（ ）
| A． | a（1+m%）2 | B． | a（1+m%）3 | C． | a（1+m%）4 | D． | （a+m%）3 |