题目内容
4.填空:(1)3$\sqrt{2}$-2$\sqrt{3}$-2$\sqrt{2}$-$\sqrt{3}$=$\sqrt{2}$-3$\sqrt{3}$;(2)9$\sqrt{3}$-$\sqrt{12}$+$\sqrt{48}$=11$\sqrt{3}$.分析 (1)直接将同类二次根式合并进而求出答案;
(2)直接化简二次根式,进而合并得出答案.
解答 解:(1)3$\sqrt{2}$-2$\sqrt{3}$-2$\sqrt{2}$-$\sqrt{3}$
=(3$\sqrt{2}$-2$\sqrt{2}$)-(2$\sqrt{3}$+$\sqrt{3}$)
=$\sqrt{2}$-3$\sqrt{3}$;
(2)9$\sqrt{3}$-$\sqrt{12}$+$\sqrt{48}$
=9$\sqrt{3}$-2$\sqrt{3}$+4$\sqrt{3}$
=11$\sqrt{3}$.
故答案为:(1)$\sqrt{2}$-3$\sqrt{3}$;(2)11$\sqrt{3}$.
点评 此题主要考查了二次根式的加减运算,正确化简二次根式是解题关键.

练习册系列答案
相关题目
12.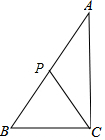 如图,△ABC是一个零件示意图,∠ACB=90°,AC=20cm,BC=15cm,从AB上取点P,与点C连结起来.以增加稳固程度.则PC的最小长度是( )
如图,△ABC是一个零件示意图,∠ACB=90°,AC=20cm,BC=15cm,从AB上取点P,与点C连结起来.以增加稳固程度.则PC的最小长度是( )
 如图,△ABC是一个零件示意图,∠ACB=90°,AC=20cm,BC=15cm,从AB上取点P,与点C连结起来.以增加稳固程度.则PC的最小长度是( )
如图,△ABC是一个零件示意图,∠ACB=90°,AC=20cm,BC=15cm,从AB上取点P,与点C连结起来.以增加稳固程度.则PC的最小长度是( )| A. | 12cm | B. | 24cm | C. | 36cm | D. | 48cm |
6.若(m-2)x${\;}^{{m}^{2}-3}$+7=0是关于x的一元一次方程,则m=( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 4 |
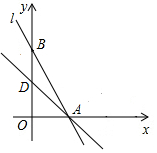 已知如图,在平面直角坐标系中,直线AB分别与x轴、y轴交于A、B两点(OA<OB),且OA、OB的长分别是一元二次方程x2-18x+72=0的两根,点D为线段OB的中点,过点D作AB的垂线与线段AB相交于点C.
已知如图,在平面直角坐标系中,直线AB分别与x轴、y轴交于A、B两点(OA<OB),且OA、OB的长分别是一元二次方程x2-18x+72=0的两根,点D为线段OB的中点,过点D作AB的垂线与线段AB相交于点C.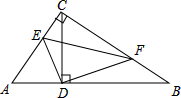 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E、F分别是AC、BC边上的点,且CE=$\frac{1}{3}$AC,BF=$\frac{1}{3}$BC.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E、F分别是AC、BC边上的点,且CE=$\frac{1}{3}$AC,BF=$\frac{1}{3}$BC.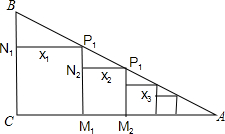 如图,在Rt△ABC中,∠C=90°,BC=a0,∠A=θ(其中a0,θ为常数),把边长依次为a1,a2,a3,…,a10的10个正方形依次放入Rt△ABC中,第一个正方形CM1P1N1的顶点分别放在Rt△ABC的各边上;第二个正方形M1M2P2N2的顶点分别放在Rt△AP1M1的各边上,…,其他正方形依次放入,则第10个正方形的边长a10=a0($\frac{1}{1+tanθ}$)10.(用a0,θ表示)
如图,在Rt△ABC中,∠C=90°,BC=a0,∠A=θ(其中a0,θ为常数),把边长依次为a1,a2,a3,…,a10的10个正方形依次放入Rt△ABC中,第一个正方形CM1P1N1的顶点分别放在Rt△ABC的各边上;第二个正方形M1M2P2N2的顶点分别放在Rt△AP1M1的各边上,…,其他正方形依次放入,则第10个正方形的边长a10=a0($\frac{1}{1+tanθ}$)10.(用a0,θ表示)