题目内容
3.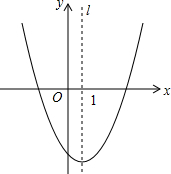 二次函数y=ax2+bx+c图象如图所示,下列正确的个数为( )
二次函数y=ax2+bx+c图象如图所示,下列正确的个数为( )①bc>0
②2a-3c<0
③2a+b>0
④ax2+bx+c=0有两个解x1,x2,x1>0,x2<0
⑤a+b+c>0
⑥当x>1时,y随x增大而增大.
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 由抛物线开口向上知a>0,由对称轴在y轴右侧知b<0,由与y轴的交点为在y轴的负半轴上得到c<0,所以判定①正确;
由a>0,c<0,利用不等式的性质判定②错误;
由对称轴为x=$\frac{-b}{2a}$=1,得2a+b=0,可以判定③错误;
由抛物线与x轴的两个交点位置,可以判定④正确;
由当x=1时,y=a+b+c<0,可以判定⑤错误;
根据二次函数的性质,可以判定⑥正确.
所以①④⑥正确.
解答 解:∵抛物线的开口向上,
∴a>0,
∵对称轴在y轴右侧,
∴-$\frac{b}{2a}$>0,
∴b<0,
∵与y轴的交点为在y轴的负半轴上,
∴c<0,
∴bc>0,
∴①正确;
∵a>0,c<0,
∴2a>0,-3c>0,
∴2a-3c>0,
∴②错误;
∵对称轴为x=$\frac{-b}{2a}$=1,
∴2a+b=0,
∴③错误;
∵抛物线y=ax2+bx+c与x轴交点横坐标的值即为方程ax2+bx+c=0的解,
由图形可知,一个交点在x轴正半轴上,一个交点在x轴负半轴上,
∴ax2+bx+c=0有两个解x1,x2,x1>0,x2<0,
∴④正确;
∵当x=1时,y=a+b+c<0,
∴⑤错误;
∵a>0,对称轴为x=1,
∴当x>1时,y随x增大而增大,
∴⑥正确.
综上所述,①④⑥正确.
故选A.
点评 本题考查了二次函数图象与系数之间的关系,二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左侧;当a与b异号时(即ab<0),对称轴在y轴右侧(简称:左同右异);常数项c决定抛物线与y轴交点,抛物线与y轴交于(0,c).抛物线与x轴交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.同时考查了不等式的性质,二次函数与一元二次方程的关系.

| A. | $\sqrt{-7}$ | B. | $\root{3}{2m}$ | C. | $\sqrt{{x^2}+1}$ | D. | $\sqrt{a}$ |
 老师出了如下的题:如图,要求在图中按下面的语言继续画图:(画图工具和方法不限)过A点画AD⊥BC于D,过D点画DE∥AB交AC于E,在线段AB上任取一点F,以F为顶点,FB为一边,画∠BFG=∠ADE,∠BFG的另一边FG与线段BC交于点G.请你按照上面画图时给出的条件说明FG⊥BC.
老师出了如下的题:如图,要求在图中按下面的语言继续画图:(画图工具和方法不限)过A点画AD⊥BC于D,过D点画DE∥AB交AC于E,在线段AB上任取一点F,以F为顶点,FB为一边,画∠BFG=∠ADE,∠BFG的另一边FG与线段BC交于点G.请你按照上面画图时给出的条件说明FG⊥BC.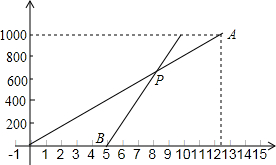 小明每天早上步行到学校上学,一天,小明从家里出发后5分钟,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,设小明离开家的时间为x(分),如图所示的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系.请分析图中的信息解答下列问题:
小明每天早上步行到学校上学,一天,小明从家里出发后5分钟,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,设小明离开家的时间为x(分),如图所示的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系.请分析图中的信息解答下列问题: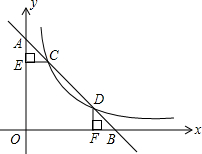 如图,一次函数的图象与x轴,y轴交于点B,A,与反比例函数y=$\frac{12}{x}$在第一象限内的图象交于点C(m,m+1),D(n,2),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.
如图,一次函数的图象与x轴,y轴交于点B,A,与反比例函数y=$\frac{12}{x}$在第一象限内的图象交于点C(m,m+1),D(n,2),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.