题目内容
7.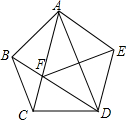 如图,在正五边形ABCDE中,连接AC、AD、BD、AC与BD相交于点F,连接EF,对于下列四种说法:
如图,在正五边形ABCDE中,连接AC、AD、BD、AC与BD相交于点F,连接EF,对于下列四种说法:①四边形AFDE是菱形;②△ABF的周长=AB+AC;③AF平分∠BFE;④CD2=CF•CA
正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①首先由正五边形的性质可得AB=BC=CD=DE=AE,AC∥ED,BD∥AE,AE=DE,根据有一组邻边相等的平行四边形是菱形即可证;②由正五边形的性质可得AC=BD,由四边形AFDE是菱形,易得AE=AF=AB=DF,BF=CF,△ABF的周长=AB+AF+BF=AB+AF+CF=AB+AC;③由四边形AFDE是菱形,易得∠AFE=∠DEF,∠AFB=∠EDF,由正五边形的性质得∠AED=108°,∠FED=∠EFD=54°,∠EDF=72°,可得∠AFE≠∠AFB,证得结论;④可证△CAD∽△CDF,由相似三角形的性质$\frac{CA}{CD}=\frac{CD}{CF}$,易得结论.
解答 解:①∵五边形ABCDE是正五边形,
∴AB=BC=CD=DE=AE,AC∥DE,BD∥AE,
∴四边形AEDF是平行四边形,
∵AE=DE,
∴四边形AFDE是菱形,
故此选项正确;
②由正五边形的性质可得AC=BD,
∵四边形AFDE是菱形,
∴AE=AF=AB=DF,
∴BF=CF,
∴△ABF的周长=AB+AF+BF=AB+AF+CF=AB+AC,
故此选项正确;
③∵四边形AFDE是菱形,
∴∠AFE=∠DEF,∠AFB=∠EDF,
∵五边形ABCDE是正五边形,
∴∠AED=108°,
∴∠FED=∠EFD=54°,∠EDF=72°,
∴∠AFE≠∠AFB,
故此选项错误;
④∵五边形ABCDE是正五边形,四边形AFDE是菱形,
∴DF=DC,AC=AD
∴∠DCF=∠DFC,∠ACD=∠ADC,
∵∠FAE=∠EDF=72°,∠CDE=108°,
∴∠CDF=36°,∠CAD=36°,
∴∠DCF=∠DFC=72°,
∴∠CAD=∠CDF,∠DCF=∠ACD,
∴△CAD∽△CDF,
∴$\frac{CA}{CD}=\frac{CD}{CF}$,
∴CD2=CF•CA,
故此选项正确,
正确的说法有:①②④,共3个.
故选C.
点评 本题考查了正五边形的性质,全等三角形的判定,综合考察的知识点较多,解答本题注意已经证明的结论,可以直接拿来使用.

 如图,如果从半径为9cm的圆形纸片剪去$\frac{1}{3}$圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面半径为( )
如图,如果从半径为9cm的圆形纸片剪去$\frac{1}{3}$圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面半径为( )| A. | 6cm | B. | 3cm | C. | 5$\sqrt{3}$cm | D. | 3$\sqrt{5}$cm |
| A. | m=9,n=-4 | B. | m=3,n=4 | C. | m=4,n=3 | D. | m=9,n=6 |
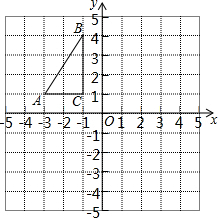 如图,网格图中每个小正方形的边长为1个单位,△ABC的顶点均在格点上,建立如图所示的平面直角坐标系
如图,网格图中每个小正方形的边长为1个单位,△ABC的顶点均在格点上,建立如图所示的平面直角坐标系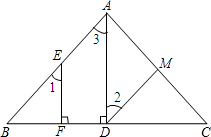 如图,已知AD⊥BC,EF⊥BC,∠1=∠2,∠BAC=80°,求∠AMD的度数.
如图,已知AD⊥BC,EF⊥BC,∠1=∠2,∠BAC=80°,求∠AMD的度数. 如图是某种标志的一部分,其对称中心是点A,请画全图形.
如图是某种标志的一部分,其对称中心是点A,请画全图形.