题目内容
19.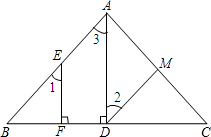 如图,已知AD⊥BC,EF⊥BC,∠1=∠2,∠BAC=80°,求∠AMD的度数.
如图,已知AD⊥BC,EF⊥BC,∠1=∠2,∠BAC=80°,求∠AMD的度数.解:∵AD⊥BC,EF⊥BC(已知),
∴AD∥EF,
∴∠1=∠3(两直线平行,同位角相等).
又∵∠1=∠2(已知),
∴∠2=∠3(等量代换),
∴AB∥DM(内错角相等,两直线平行),
∴∠BAC+∠AMD=180°(两直线平行,同旁内角互补),
又∵∠BAC=80°,
∴∠AMD=180°-80°=100°.
分析 根据平行线的判定得出AD∥EF,根据平行线的性质得出∠1=∠3,求出∠2=∠3,根据平行线的判定得出AB∥DM即可.
解答 解:∵AD⊥BC,EF⊥BC(已知),
∴AD∥EF,
∴∠1=∠3(两直线平行,同位角相等).
又∵∠1=∠2(已知),
∴∠2=∠3(等量代换),
∴AB∥DM(内错角相等,两直线平行),
∴∠BAC+∠AMD=180°(两直线平行,同旁内角互补),
又∵∠BAC=80°,
∴∠AMD=180°-80°=100°,
故答案为:EF,∠1,两直线平行,同位角相等,∠3,等量代换,AB,DM,∠AMD,两直线平行,同旁内角互补.
点评 本题考查了平行线的性质和判定的应用,能正确运用定理进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.一元二次方程x(x-5)=0的解是( )
| A. | x=0或x=5 | B. | x=0 | C. | x=5 | D. | x=0或x=-5 |
7.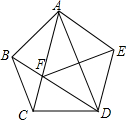 如图,在正五边形ABCDE中,连接AC、AD、BD、AC与BD相交于点F,连接EF,对于下列四种说法:
如图,在正五边形ABCDE中,连接AC、AD、BD、AC与BD相交于点F,连接EF,对于下列四种说法:
①四边形AFDE是菱形;②△ABF的周长=AB+AC;③AF平分∠BFE;④CD2=CF•CA
正确的有( )
 如图,在正五边形ABCDE中,连接AC、AD、BD、AC与BD相交于点F,连接EF,对于下列四种说法:
如图,在正五边形ABCDE中,连接AC、AD、BD、AC与BD相交于点F,连接EF,对于下列四种说法:①四边形AFDE是菱形;②△ABF的周长=AB+AC;③AF平分∠BFE;④CD2=CF•CA
正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14. 如图,直线a∥b∥c,∠1=100°,∠2=135°,那么∠α等于( )
如图,直线a∥b∥c,∠1=100°,∠2=135°,那么∠α等于( )
 如图,直线a∥b∥c,∠1=100°,∠2=135°,那么∠α等于( )
如图,直线a∥b∥c,∠1=100°,∠2=135°,那么∠α等于( )| A. | 45° | B. | 55° | C. | 60° | D. | 70° |
11.下列四个命题中是真命题的是( )
| A. | 相等的角是对顶角 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 实数与数轴上的点是一一对应的 | |
| D. | 垂直于同一条直线的两条直线互相平行 |