题目内容
17.(1)如图1,△ABC中,AB=AC,P为BC上任一点,PE⊥AB于E,PF⊥AC于F,BM⊥AC于M.求证:PE+PF=BM.(2)应用:如图2所示,已知菱形ABCD的对角线的交点为O,AC=2,∠BAD=60°,BD边上有2016个不同的点P1,P2,P3,…P2016,过点Pi(i=1,2,3,…2016)作PiEi⊥AB于Ei,PiFi⊥AC于Fi.计算P1E1+P1F1+P2E2+P2F2+…+P2016E2016+P2016F2016的值.
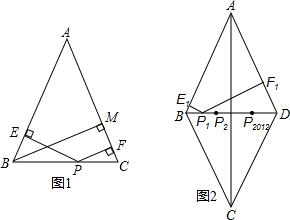
分析 (1)连接AP,可分别表示出△ABC、△ABP、△ACP的面积,根据面积相等可证得结论;
(2)连接AP1,根据菱形性质得出AB=AD,AO=OC=$\frac{1}{2}$AC=1,AC⊥BD,得出等边三角形ABD,推出AD=AB=BD,根据三角形面积公式求出P1E1+P1F1=P2E2+P2F2=P3E3+P3F3=P4E4+P4F4=…=AO=1,求出即可.
解答 (1)证明:连结AP,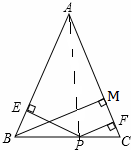 ∵PE⊥AB PF⊥AC BM⊥AC
∵PE⊥AB PF⊥AC BM⊥AC
∴S△ABP=$\frac{1}{2}$AB×PE,S△ACP=$\frac{1}{2}$AC×PF
S△ABC=$\frac{1}{2}$AC×BM,
∵S△ABP+S△ACP=S△ABC
∴$\frac{1}{2}$AB×PE+$\frac{1}{2}$AC×PF=$\frac{1}{2}$AC×BM,
∵AB=AC
∴PE+PF=BM;
(2)解:连接P1A,设AC与BD相交于点O,
∵四边形ABCD是菱形,
∴AB=AD,AO=OC=AC=$\frac{1}{2}$×2=1,AC⊥BD,
∵AB=AD,∠BAD=60°,
∴△ABD是等边三角形,
∴AB=BD=AD,
∵S△ABD=S△ABP1+S△ADP1,
∴$\frac{1}{2}$×BD×AO=$\frac{1}{2}$AB×P1E1+$\frac{1}{2}$×AD×P1F1,
∴P1E1+P1F1=AO=1,
同理P2E2+P2F2=P3E3+P3F3=P4E4+P4F4=…=AO=1,
∴P1E1+P1F1+P2E2+P2F2+…P2016E2016+P2016F2016的值为2016×1=2016.
点评 (1)本题主要考查等边三角形的性质及等积法,利用等积法得到AB•PE+AC•PF=AC•BM是解题的关键.
(2)本题考查了菱形的性质,等边三角形的性质和判定,三角形的面积的应用,关键是求出P1E1+P1F1=P2E2+P2F2=P3E3+P3F3=P4E4+P4F4=…=AO=1.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
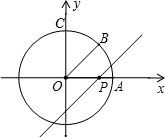 如图,⊙O是以数轴原点O为圆心,半径为3的圆,与坐标轴的正半轴分别交于A、C两点,OB平分∠AOC,点P在数轴上运动,过点P且与OB平行的直线与⊙O有公共点,则线段OP的取值范围是0<OP≤3$\sqrt{2}$.
如图,⊙O是以数轴原点O为圆心,半径为3的圆,与坐标轴的正半轴分别交于A、C两点,OB平分∠AOC,点P在数轴上运动,过点P且与OB平行的直线与⊙O有公共点,则线段OP的取值范围是0<OP≤3$\sqrt{2}$. 如图,在五边形ABCDE中,已知∠BAE=120°,∠B=∠E=90°,AB=BC=2,AE=DE=4,在BC、DE上分别找一点M、N,若要使△AMN的周长最小时,则△AMN的最小周长为4$\sqrt{7}$.
如图,在五边形ABCDE中,已知∠BAE=120°,∠B=∠E=90°,AB=BC=2,AE=DE=4,在BC、DE上分别找一点M、N,若要使△AMN的周长最小时,则△AMN的最小周长为4$\sqrt{7}$. 某天,小华到学校时发现有物品遗忘在家中,此时离上课还有15分钟,于是立即步行回家去取.同时,他爸爸从家里出发骑自行车以他3倍的速度给他送遗忘的物品,两人在途中相遇,相遇后小华立即坐爸爸的自行车赶回学校.爸爸和小华在这个过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系如图所示(假设骑自行车和步行的速度始终保持不变).下列说法:
某天,小华到学校时发现有物品遗忘在家中,此时离上课还有15分钟,于是立即步行回家去取.同时,他爸爸从家里出发骑自行车以他3倍的速度给他送遗忘的物品,两人在途中相遇,相遇后小华立即坐爸爸的自行车赶回学校.爸爸和小华在这个过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系如图所示(假设骑自行车和步行的速度始终保持不变).下列说法: 已知∠ACD=150°,∠B=120°,求∠A.
已知∠ACD=150°,∠B=120°,求∠A.