题目内容
8.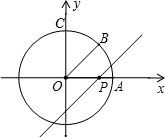 如图,⊙O是以数轴原点O为圆心,半径为3的圆,与坐标轴的正半轴分别交于A、C两点,OB平分∠AOC,点P在数轴上运动,过点P且与OB平行的直线与⊙O有公共点,则线段OP的取值范围是0<OP≤3$\sqrt{2}$.
如图,⊙O是以数轴原点O为圆心,半径为3的圆,与坐标轴的正半轴分别交于A、C两点,OB平分∠AOC,点P在数轴上运动,过点P且与OB平行的直线与⊙O有公共点,则线段OP的取值范围是0<OP≤3$\sqrt{2}$.
分析 点P与⊙O相切时,OP取得极值,作出切线,利用切线的性质求解即可.
解答  解:将OA平移至P'D的位置,使P'D与圆相切,
解:将OA平移至P'D的位置,使P'D与圆相切,
连接OD,由题意得,OD=3,∠DOP'=45°,∠ODP'=90°,
故可得OP'=3$\sqrt{2}$,即OP的极大值为3$\sqrt{2}$,
故答案为:0<OP≤3$\sqrt{2}$.
点评 本题考查了直线与圆的位置关系问题.关键是通过平移,确定直线与圆相切的情况,求出此时OP的值.

练习册系列答案
相关题目
3.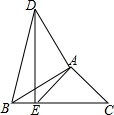 如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )
如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )
 如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )
如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
13.若分式方程$\frac{1}{x-1}$+3=$\frac{b-x}{a+x}$有增根,则a的值是( )
| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
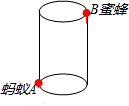 如图,圆柱形容器高12cm,底面周长24cm,在杯口点B处有一滴蜂蜜,此时蚂蚁在杯外壁底部与蜂蜜相对的A处,
如图,圆柱形容器高12cm,底面周长24cm,在杯口点B处有一滴蜂蜜,此时蚂蚁在杯外壁底部与蜂蜜相对的A处, 如图,Rt△ABC≌Rt△DBF,∠ACB=∠DFB=90°,∠D=28°,求∠GBF的度数.
如图,Rt△ABC≌Rt△DBF,∠ACB=∠DFB=90°,∠D=28°,求∠GBF的度数.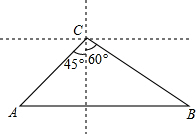 如图,一条城际铁路从A市到B市需要经过C市,A市位于C市西南方向,与C市相距40在千米,B市恰好位于A市的正东方向和C市的南偏东60°方向处.因打造城市经济新格局需要,将从A市到B市之间铺设一条笔直的铁路,求新铺设的铁路AB的长度.(结果保留根号)
如图,一条城际铁路从A市到B市需要经过C市,A市位于C市西南方向,与C市相距40在千米,B市恰好位于A市的正东方向和C市的南偏东60°方向处.因打造城市经济新格局需要,将从A市到B市之间铺设一条笔直的铁路,求新铺设的铁路AB的长度.(结果保留根号)