题目内容
2.定义:图象开口方向相同,且都经过同一点的所有二次函数称为共点二次函数系,比如函数y=2x2+bx+c,当b+c=1时,它们的图象都经过定点(1,3),且开口都向上,称所有二次函数y=2x2+bx+c为共点(1,3)开口向上的二次函数系.(1)已知二次函数y=ax2+bx+c(c≠0)与y=x2-2x+n是共点二次函数,当a+b+c=1时,求n的值;
(2)已知函数y=x2+bx+c图象过定点(-2,1),且开口向上的共点二次函数系,试求该二次函数系的最小值能够达到的最大结果.
分析 (1)由当x=1时函数值为y=a+b+c=1,得出共点坐标为(1,1),代入y=x2-2x+n即可求得n;
(2)把(-2,1)代入y=x2+bx+c求得c=2b-3,根据最小值的公式得出最小值=-$\frac{1}{4}$(b-4)2+1≤1,即可求得最小值能够达到的最大结果.
解答 解(1)二次函数y=ax2+bx+c(c≠0)当x=1时y=a+b+c,
∵a+b+c=1,
∴共点为(1,1),
代入y=x2-2x+n得,1=1-2+n,解得n=2;
(2)把(-2,1)代入y=x2+bx+c得,1=4-2b+c,
则c=2b-3,
二次函数的最小值为$\frac{4ac-{b}^{2}}{4a}$=$\frac{4(2b-3)-{b}^{2}}{4}$=-$\frac{1}{4}$b2+2b-3=-$\frac{1}{4}$(b-4)2+1≤1,
故该二次函数系的最小值能够达到的最大结果是1.
点评 本题考查了二次函数的性质,二次函数图象上点的坐标特征,熟练掌握函数的顶点公式是解题的关键.

练习册系列答案
相关题目
13.若分式方程$\frac{1}{x-1}$+3=$\frac{b-x}{a+x}$有增根,则a的值是( )
| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
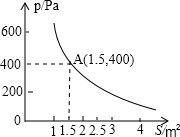 某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.
某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.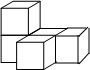 如图所示的几何体是由五个小正方体组合而成的,它的左视图是( )
如图所示的几何体是由五个小正方体组合而成的,它的左视图是( )


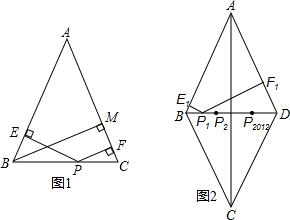
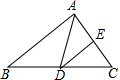 如图,已知S△ABC=8cm2,AD是中线,DE是△ADC的中线,则S△ADE=2cm2.
如图,已知S△ABC=8cm2,AD是中线,DE是△ADC的中线,则S△ADE=2cm2.