题目内容
18.若$\root{3}{0.3670}$=0.7160,则$\root{3}{367}$=7.160.已知$\sqrt{102.01}$=10.1,则$\sqrt{1.0201}$=1.01.分析 依据被开方数小数点向左或向右移动3为对应的立方根的小数点向左或向右移动1或根据算术平方根的移动规律,把被开方数的小数点每移动两位,结果移动一位,求解即可.
解答 解:∵$\root{3}{0.3670}$=0.7160,则$\root{3}{367}$=7.160,
∵$\sqrt{102.01}$=10.1,则$\sqrt{1.0201}$=1.01,
故答案为:7.160,1.01.
点评 本题考查了算术平方根和立方根的移动规律的应用,能根据移动规律填空是解此题的关键.

练习册系列答案
相关题目
8.在平面直角坐标系中,点A(3,-1)关于y轴的对称点A'的坐标是( )
| A. | (-3,-1) | B. | (3,1) | C. | (-3,1) | D. | (-1,3) |
9. 若数字a的位置如图所示,化简|1+a|+|2-a|得( )
若数字a的位置如图所示,化简|1+a|+|2-a|得( )
 若数字a的位置如图所示,化简|1+a|+|2-a|得( )
若数字a的位置如图所示,化简|1+a|+|2-a|得( )| A. | 1 | B. | -2a+1 | C. | 2a+1 | D. | 3 |
13.在用代入消元法解方程组$\left\{\begin{array}{l}{3x+y=-9}\\{4x-3y=3}\end{array}\right.$时,消去未知数y后,得到的方程为( )
| A. | 4x-3(-9-3x)=3 | B. | 4x+3(-9-3x)=3 | C. | 4x-3(-9+3x)=3 | D. | 4x+3(-9+3x)=3 |
3.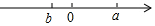 有理数a,b在数轴上的位置如图所示,则下列结论正确的是( )
有理数a,b在数轴上的位置如图所示,则下列结论正确的是( )
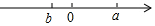 有理数a,b在数轴上的位置如图所示,则下列结论正确的是( )
有理数a,b在数轴上的位置如图所示,则下列结论正确的是( )| A. | a-b<b<a<a+b | B. | a-b<b<a+b<a | C. | b<a+b<a<a-b | D. | a+b<b<a<a-b |
7.已知△ABC~△DEF,相似比为3:1,且△ABC的面积与△DEF的面积和为20,则△DEF的面积为( )
| A. | 5 | B. | 2 | C. | 15 | D. | 18 |