Question

20．如图，平行四边形ABCD中，E为AB中点，F为AD上一点，EF交AC于点G，AF=3cm，DF=6cm，AG=4cm，则AC的长为（　　）

• A． 12cm
• B． 16cm
• C． 20cm
• D． 24cm

Answer 1

分析 首先求证出EO∥BC，得到EO=$\frac{1}{2}$BC，然后根据平行线的性质求证出△AFG∽△OEG．进而得到$\frac{AG}{OG}$=$\frac{AF}{OE}$，求出GO=6，即可得到结论．

解答 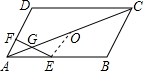解：在?ABCD中，
∵BC=AD=AF+DF=9，
设AC的中点为O，连接EO，又E是AB的中点，
∴EO∥BC，EO=$\frac{1}{2}$BC=$\frac{9}{2}$，
又AD∥BC，
∴AF∥EO，
∴△AFG∽△OEG，
∴$\frac{AG}{OG}$=$\frac{AF}{OE}$，
∴GO=6，
∴AO=AG+OG=4+6=10，
∴AC=2AO=20，
故选：C．

点评 本题主要考查了平行四边形的性质，全等三角形的判定及线段的比例问题，熟练掌握相似三角形的判定和性质是解题的关键．