题目内容
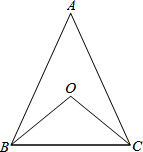 如图,△ABC中,AB=AC,∠ABC=70°,点O是△ABC的外心,则∠BOC的度数为( )
如图,△ABC中,AB=AC,∠ABC=70°,点O是△ABC的外心,则∠BOC的度数为( )| A、40° | B、60° |
| C、70° | D、80° |
考点:三角形的外接圆与外心
专题:
分析:首先根据等腰三角形的性质可得∠A的度数,然后根据圆周角定理可得∠O=2∠A,进而可得答案.
解答:解:∵AB=AC,
∴∠ABC=∠ACB=70°,
∴∠A=180°-70°×2=40°,
∵点O是△ABC的外心,
∴∠BOC=40°×2=80°,
故选:D.
∴∠ABC=∠ACB=70°,
∴∠A=180°-70°×2=40°,
∵点O是△ABC的外心,
∴∠BOC=40°×2=80°,
故选:D.
点评:此题主要考查了三角形的外接圆和外心,关键是掌握圆周角定理:在同圆或等圆中,同弧所对的圆周角等于圆心角的一半.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
下列图形经过折叠,能围成正方体的是( )
A、 |
B、 |
C、 |
D、 |
已知线段AB=3cm,延长线段AB到C,使BC=4cm,延长线段BA到D,使AD=AC,则线段CD的长为( )
| A、14cm | B、8cm |
| C、7cm | D、6cm |
 如图,把△ABC绕着顶点A逆时针旋转50°,得到△ADE,其中点B的对应点D恰好落在AC边上,点F,G分别是AC,AE上的点,AF=AG,延长BF交DG于点H.
如图,把△ABC绕着顶点A逆时针旋转50°,得到△ADE,其中点B的对应点D恰好落在AC边上,点F,G分别是AC,AE上的点,AF=AG,延长BF交DG于点H.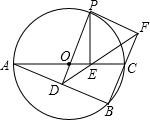 如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF.
如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF. 如图,已知点A是线段OB的垂直平分线上一点,AN⊥ON,BO⊥ON,P为ON上一点,∠OPB=∠OAB.
如图,已知点A是线段OB的垂直平分线上一点,AN⊥ON,BO⊥ON,P为ON上一点,∠OPB=∠OAB. 如图,∠ABC=∠EAC=90°,BC长为3cm,AB长为4cm,AE为12cm,求正方形CDFE的面积.
如图,∠ABC=∠EAC=90°,BC长为3cm,AB长为4cm,AE为12cm,求正方形CDFE的面积. 如图所示,已知四边形ABCD中,AB∥CD,BC⊥CD,∠A=60°,CD=
如图所示,已知四边形ABCD中,AB∥CD,BC⊥CD,∠A=60°,CD=