题目内容
 如图,已知点A是线段OB的垂直平分线上一点,AN⊥ON,BO⊥ON,P为ON上一点,∠OPB=∠OAB.
如图,已知点A是线段OB的垂直平分线上一点,AN⊥ON,BO⊥ON,P为ON上一点,∠OPB=∠OAB.(1)若∠AOB=60°,PB=4,则OP=
(2)在(1)的条件下,求证:PA+PO=PB;
(3)如图②,若ON=5,求出PO+PB的值.
考点:全等三角形的判定与性质,线段垂直平分线的性质,等边三角形的判定与性质
专题:综合题
分析:(1)易证△AOB是等边三角形,从而可得∠OPB=∠OAB=60°,即可得到∠OBP=30°,然后根据30°角所得的直角边等于斜边的一半即可求出OP的值;
(2)如图①,由(1)可得OB=AB,∠ABP=∠OBP=30°,从而可证到△OBP≌△ABP,则有OP=AP=2,即可证到PA+PO=4=PB;
(3)延长ON、BA交于点D,如图②.由AO=AB,∠DOB=90°可证到∠D=∠AOD,从而可得AD=AO,由AN⊥OD可得DN=ON=5,由∠OPB=∠OAB可得∠AOD=∠PBD,从而得到∠D=∠PBD,则有PD=PB,即可得到PO+PB=PO+PD=OD=10.
(2)如图①,由(1)可得OB=AB,∠ABP=∠OBP=30°,从而可证到△OBP≌△ABP,则有OP=AP=2,即可证到PA+PO=4=PB;
(3)延长ON、BA交于点D,如图②.由AO=AB,∠DOB=90°可证到∠D=∠AOD,从而可得AD=AO,由AN⊥OD可得DN=ON=5,由∠OPB=∠OAB可得∠AOD=∠PBD,从而得到∠D=∠PBD,则有PD=PB,即可得到PO+PB=PO+PD=OD=10.
解答:解:(1)∵点A是线段OB的垂直平分线上一点,
∴AO=AB.
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OB=AB,∠OAB=∠ABO=60°.
∴∠OPB=∠OAB=60°.
∵BO⊥ON,即∠POB=90°,
∴∠OBP=30°,
∴OP=
PB=
×4=2.
故答案为2;
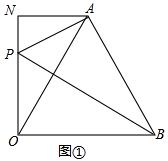
(2)证明:如图①,
由(1)得OB=AB,∠OAB=∠ABO=60°,∠OBP=30°,
∴∠ABP=∠ABO-∠OBP=30°=∠OBP.
在△OBP和△ABP中,
,
∴△OBP≌△ABP(SAS),
∴OP=AP=2,
∴PA+PO=4=PB;
(3)延长ON、BA交于点D,如图②.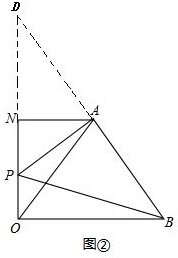
∵AO=AB,∴∠AOB=∠ABO.
∵∠DOB=90°,
∴∠D+∠OBD=90°,∠AOD+∠BOA=90°,
∴∠D=∠AOD,
∴AD=AO.
∵AN⊥OD,
∴DN=ON=5.
∵∠OPB=∠OAB,
∴∠AOD=∠PBD,
∴∠D=∠PBD,
∴PD=PB,
∴PO+PB=PO+PD=OD=10.
∴AO=AB.
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OB=AB,∠OAB=∠ABO=60°.
∴∠OPB=∠OAB=60°.
∵BO⊥ON,即∠POB=90°,
∴∠OBP=30°,
∴OP=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为2;

(2)证明:如图①,
由(1)得OB=AB,∠OAB=∠ABO=60°,∠OBP=30°,
∴∠ABP=∠ABO-∠OBP=30°=∠OBP.
在△OBP和△ABP中,
|
∴△OBP≌△ABP(SAS),
∴OP=AP=2,
∴PA+PO=4=PB;
(3)延长ON、BA交于点D,如图②.

∵AO=AB,∴∠AOB=∠ABO.
∵∠DOB=90°,
∴∠D+∠OBD=90°,∠AOD+∠BOA=90°,
∴∠D=∠AOD,
∴AD=AO.
∵AN⊥OD,
∴DN=ON=5.
∵∠OPB=∠OAB,
∴∠AOD=∠PBD,
∴∠D=∠PBD,
∴PD=PB,
∴PO+PB=PO+PD=OD=10.
点评:本题主要考查了全等三角形的判定与性质、等边三角形的判定与性质、等腰三角形的判定与性质、线段垂直平分线的性质、30°角所得的直角边等于斜边的一半、等角的余角相等等知识,证到△OBP≌△ABP是解决第(2)小题的关键,通过添加适当的辅助线将PO+PB转化为线段OD是解决第(3)小题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
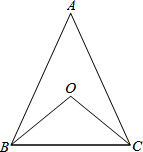 如图,△ABC中,AB=AC,∠ABC=70°,点O是△ABC的外心,则∠BOC的度数为( )
如图,△ABC中,AB=AC,∠ABC=70°,点O是△ABC的外心,则∠BOC的度数为( )| A、40° | B、60° |
| C、70° | D、80° |
在下列各数-(+3)、-22、-
、-(-1)、2014、-|-4|中,负数的个数是( )
| 32 |
| 4 |
| A、2 | B、3 | C、4 | D、5 |




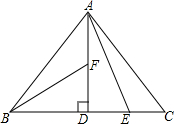 如图,在Rt△ABC中,AB=AC,AD⊥BC,垂足为D.E、F分别是CD、AD上的点,且CE=AF.如果∠AED=62°,求∠DBF的度数.
如图,在Rt△ABC中,AB=AC,AD⊥BC,垂足为D.E、F分别是CD、AD上的点,且CE=AF.如果∠AED=62°,求∠DBF的度数. 小昆和小明玩摸牌游戏,游戏规则如下,有3张背面完全相同,牌面标有数字1、2、3的纸牌,将纸牌洗匀后背面朝上放在桌子上,随机抽出一张,记下牌面数字,再从剩下的牌中抽出一张,两次抽到的牌分别记为A、B.
小昆和小明玩摸牌游戏,游戏规则如下,有3张背面完全相同,牌面标有数字1、2、3的纸牌,将纸牌洗匀后背面朝上放在桌子上,随机抽出一张,记下牌面数字,再从剩下的牌中抽出一张,两次抽到的牌分别记为A、B. 如图,在∠1到∠6的六个角中,同位角有
如图,在∠1到∠6的六个角中,同位角有