题目内容
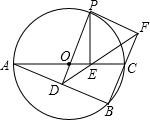 如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF.
如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF.(1)求证:△ADO≌△PEO;
(2)若∠OAD=30°,劣弧PC长为2π,求AC的长度.
考点:三角形的外接圆与外心,全等三角形的判定与性质,弧长的计算
专题:
分析:(1)直接利用AAS得出△POE≌△AOD即可得出答案;
(2)利用弧长公式进而求出圆的半径,即可得出AC的长.
(2)利用弧长公式进而求出圆的半径,即可得出AC的长.
解答:(1)证明:∵PE⊥AC,OD⊥AB,
∠PEA=90°,∠ADO=90°
在△ADO和△PEO中,
∵
,
∴△POE≌△AOD(AAS);
(2)解:∵∠OAD=30°,∠ADO=90°,
∴∠AOD=∠POE=60°,
∵劣弧PC长为2π,
∴
=2π,
∴OP=6,
∴AC的长度为:12.
∠PEA=90°,∠ADO=90°
在△ADO和△PEO中,
∵
|

∴△POE≌△AOD(AAS);
(2)解:∵∠OAD=30°,∠ADO=90°,
∴∠AOD=∠POE=60°,
∵劣弧PC长为2π,
∴
| 60π•OP |
| 180 |
∴OP=6,
∴AC的长度为:12.
点评:此题主要考查了全等三角形的判定与性质以及弧长公式等知识,得出∠POE=60°是解题关键.

练习册系列答案
相关题目
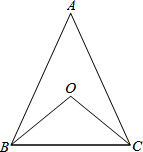 如图,△ABC中,AB=AC,∠ABC=70°,点O是△ABC的外心,则∠BOC的度数为( )
如图,△ABC中,AB=AC,∠ABC=70°,点O是△ABC的外心,则∠BOC的度数为( )| A、40° | B、60° |
| C、70° | D、80° |
 如图,在方格纸中,我们把每个小正方形的顶点称为格点.己知点A、B、C都在格点上,且每个小正方形的边长都为1.
如图,在方格纸中,我们把每个小正方形的顶点称为格点.己知点A、B、C都在格点上,且每个小正方形的边长都为1.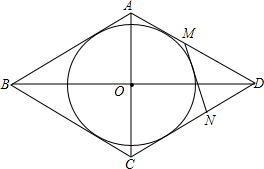 如图,已知菱形ABCD外切于圆O,MN是与AD、CD分别交于M、N的任意一条切线.求证:AM•CN为定值.
如图,已知菱形ABCD外切于圆O,MN是与AD、CD分别交于M、N的任意一条切线.求证:AM•CN为定值.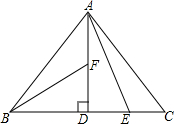 如图,在Rt△ABC中,AB=AC,AD⊥BC,垂足为D.E、F分别是CD、AD上的点,且CE=AF.如果∠AED=62°,求∠DBF的度数.
如图,在Rt△ABC中,AB=AC,AD⊥BC,垂足为D.E、F分别是CD、AD上的点,且CE=AF.如果∠AED=62°,求∠DBF的度数. 如图,已知点D为线段AC的中点,点B为线段DC的中点,DB=2,则线段AC=
如图,已知点D为线段AC的中点,点B为线段DC的中点,DB=2,则线段AC=