题目内容
 如图所示,已知四边形ABCD中,AB∥CD,BC⊥CD,∠A=60°,CD=
如图所示,已知四边形ABCD中,AB∥CD,BC⊥CD,∠A=60°,CD=| 3 |
考点:解直角三角形,等边三角形的判定与性质
专题:
分析:过D作DE⊥AB于E,求出DE∥BC,推出四边形DEBC是矩形,根据矩形的性质得出DC=BE=
cm,DE=BC=3cm,解直角三角形求出即可.
| 3 |
解答:解:
过D作DE⊥AB于E,
则∠DEA=∠DEB=90°,
∵BC⊥CD,
∴∠B=∠DEA=90°,
∴DE∥BC,
∵DC∥AB,
∴四边形DEBC是矩形,
∴DC=BE=
cm,DE=BC=3cm,
∵∠A=60°,
∴AE=
=1cm,
∴AB=BE+AE=3cm+1cm=4cm.

过D作DE⊥AB于E,
则∠DEA=∠DEB=90°,
∵BC⊥CD,
∴∠B=∠DEA=90°,
∴DE∥BC,
∵DC∥AB,
∴四边形DEBC是矩形,
∴DC=BE=
| 3 |
∵∠A=60°,
∴AE=
| DE |
| tan60° |
∴AB=BE+AE=3cm+1cm=4cm.
点评:本题考查了解再见三角形,矩形的性质和判定,直角梯形的应用,解此题的关键是能把梯形转化成矩形和直角三角形,难度适中.

练习册系列答案
相关题目
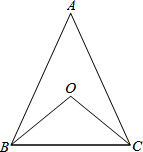 如图,△ABC中,AB=AC,∠ABC=70°,点O是△ABC的外心,则∠BOC的度数为( )
如图,△ABC中,AB=AC,∠ABC=70°,点O是△ABC的外心,则∠BOC的度数为( )| A、40° | B、60° |
| C、70° | D、80° |
 如图,在方格纸中,我们把每个小正方形的顶点称为格点.己知点A、B、C都在格点上,且每个小正方形的边长都为1.
如图,在方格纸中,我们把每个小正方形的顶点称为格点.己知点A、B、C都在格点上,且每个小正方形的边长都为1.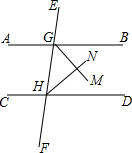 如图,已知GM,HN分别平分∠BGH,∠GHD,GM⊥HN,求证:AB∥CD.
如图,已知GM,HN分别平分∠BGH,∠GHD,GM⊥HN,求证:AB∥CD. 如图,在∠1到∠6的六个角中,同位角有
如图,在∠1到∠6的六个角中,同位角有 如图,已知点D为线段AC的中点,点B为线段DC的中点,DB=2,则线段AC=
如图,已知点D为线段AC的中点,点B为线段DC的中点,DB=2,则线段AC=