题目内容
 如图,把△ABC绕着顶点A逆时针旋转50°,得到△ADE,其中点B的对应点D恰好落在AC边上,点F,G分别是AC,AE上的点,AF=AG,延长BF交DG于点H.
如图,把△ABC绕着顶点A逆时针旋转50°,得到△ADE,其中点B的对应点D恰好落在AC边上,点F,G分别是AC,AE上的点,AF=AG,延长BF交DG于点H.(1)求证:BF=DG;
(2)求∠FHG的度数.
考点:旋转的性质
专题:
分析:(1)如图,证明△ABF≌△ADG,得到BF=DG,即可解决问题.
(2)证明∠ABF+∠AGH=∠ADG+∠AGH,此为解题的关键性结论;求出∠ABF+∠AGH=130°,∠BAG=100°,即可解决问题.
(2)证明∠ABF+∠AGH=∠ADG+∠AGH,此为解题的关键性结论;求出∠ABF+∠AGH=130°,∠BAG=100°,即可解决问题.
解答: 证明(1):由题意得:
证明(1):由题意得:
△ABC≌△ADE,
∴∠BAF=∠DAG,AB=AD;
在△ABF与△ADG中,
,
∴△ABF≌△ADG(SAS),
∴BF=DG.
(2)∵△ABF≌△ADG,
∴∠ABF=∠ADG,
∴∠ABF+∠AGH=∠ADG+∠AGH;
由题意得:∠BAF=∠DAG=50°,
∴∠ABF+∠AGH=∠ADG+∠AGH
=180°-50°=130°,
∴∠FHG=∠BHG=360°-130°-100°
=130°.
 证明(1):由题意得:
证明(1):由题意得:△ABC≌△ADE,
∴∠BAF=∠DAG,AB=AD;
在△ABF与△ADG中,
|
∴△ABF≌△ADG(SAS),
∴BF=DG.
(2)∵△ABF≌△ADG,
∴∠ABF=∠ADG,
∴∠ABF+∠AGH=∠ADG+∠AGH;
由题意得:∠BAF=∠DAG=50°,
∴∠ABF+∠AGH=∠ADG+∠AGH
=180°-50°=130°,
∴∠FHG=∠BHG=360°-130°-100°
=130°.
点评:该题主要考查了旋转变换的性质、全等三角形的判定及其性质等几何知识点及其应用问题;解题的关键是深入观察图形结构特点,准确找出图形中隐含的等量关系.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
某种商品的进价为1000元,出售时的标价为1500元,后来由于该商品积压,商店准备打折出售,但要保持利润率不低于5%,则至少可打( )
| A、6折 | B、7折 | C、8折 | D、9折 |
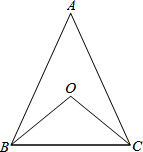 如图,△ABC中,AB=AC,∠ABC=70°,点O是△ABC的外心,则∠BOC的度数为( )
如图,△ABC中,AB=AC,∠ABC=70°,点O是△ABC的外心,则∠BOC的度数为( )| A、40° | B、60° |
| C、70° | D、80° |

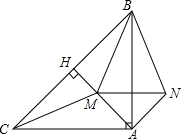 如图,在△ABC中,∠BAC=90°,AB=AC,AH⊥BC于点H,M为线段AH上一点(与A,H不重合)连CM,BM.
如图,在△ABC中,∠BAC=90°,AB=AC,AH⊥BC于点H,M为线段AH上一点(与A,H不重合)连CM,BM.



 如图,在方格纸中,我们把每个小正方形的顶点称为格点.己知点A、B、C都在格点上,且每个小正方形的边长都为1.
如图,在方格纸中,我们把每个小正方形的顶点称为格点.己知点A、B、C都在格点上,且每个小正方形的边长都为1.