题目内容
星期天,小明下午4点到5点之间外出购买文具.离开家时和回到家时,都发现时钟的时针分针相互垂直,他外出的时间共 分钟.
考点:一元一次方程的应用,钟面角
专题:
分析:根据题意,设小明外出到回家时针走了x°,则分针走了(2×90°+x°),可得到时针的度数,又因为时针每分钟走0.5°,故小明外出用的时间可求.
解答:解:设时针从小明外出到回家走了x°,则分针走了(2×90°+x°),
由题意,得
=
,
解得x=(
)°,
因时针每分钟走0.5°,
÷0.5=
(分钟).
则他外出的时间共
分钟.
故答案为:
.
由题意,得
| 180°+x° |
| 360° |
| x° |
| 30° |
解得x=(
| 180 |
| 11 |
因时针每分钟走0.5°,
| 180 |
| 11 |
| 360 |
| 11 |
则他外出的时间共
| 360 |
| 11 |
故答案为:
| 360 |
| 11 |
点评:本题考查一元一次方程的应用,钟表时针与分针的夹角.在钟表问题中,常利用时针与分针转动的度数关系:分针每转动1°时针转动(
)°,并且利用起点时间时针和分针的位置关系建立方程的数学模型.
| 1 |
| 12 |

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
若a-2b-3=0,则(a-2b)2-a+2b-5的值是( )
| A、-5 | B、-11 | C、7 | D、1 |
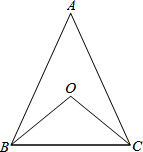 如图,△ABC中,AB=AC,∠ABC=70°,点O是△ABC的外心,则∠BOC的度数为( )
如图,△ABC中,AB=AC,∠ABC=70°,点O是△ABC的外心,则∠BOC的度数为( )| A、40° | B、60° |
| C、70° | D、80° |
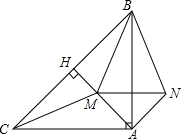 如图,在△ABC中,∠BAC=90°,AB=AC,AH⊥BC于点H,M为线段AH上一点(与A,H不重合)连CM,BM.
如图,在△ABC中,∠BAC=90°,AB=AC,AH⊥BC于点H,M为线段AH上一点(与A,H不重合)连CM,BM.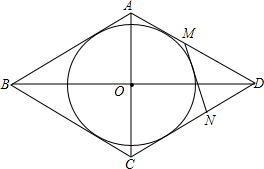 如图,已知菱形ABCD外切于圆O,MN是与AD、CD分别交于M、N的任意一条切线.求证:AM•CN为定值.
如图,已知菱形ABCD外切于圆O,MN是与AD、CD分别交于M、N的任意一条切线.求证:AM•CN为定值. 如图所示,正方形ABCD中,M是AD的中点,点N在DC上,且DN=
如图所示,正方形ABCD中,M是AD的中点,点N在DC上,且DN=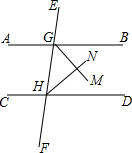 如图,已知GM,HN分别平分∠BGH,∠GHD,GM⊥HN,求证:AB∥CD.
如图,已知GM,HN分别平分∠BGH,∠GHD,GM⊥HN,求证:AB∥CD. 已知,如图,点E是BC延长线上一点,AE交CD于点F,AB∥CD,∠1=∠2,∠3=∠4.求证:AD∥BE.
已知,如图,点E是BC延长线上一点,AE交CD于点F,AB∥CD,∠1=∠2,∠3=∠4.求证:AD∥BE.