题目内容
1.化简分式$\frac{1-x}{{x}^{2}-1}$+$\frac{x}{{x}^{2}+x}$的结果为0.分析 先根据约分法则把原式变形,再根据异分母分式的加减法运算法则计算即可.
解答 解:原式=$\frac{1-x}{(x+1)(x-1)}$+$\frac{x}{x(x+1)}$
=-$\frac{1}{x+1}$+$\frac{x}{x(x+1)}$
=-$\frac{x}{x(x+1)}$+$\frac{x}{x(x+1)}$
=0.
点评 本题考查的是分式的加减法运算,掌握分式的约分法则和通分法则是解题的关键.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
16.如果∠2是∠1的余角,∠3是∠1的补角,那么∠2和∠3的关系是( )
| A. | ∠3-∠2=90° | B. | ∠3+∠2=90° | C. | ∠3=∠2 | D. | 没有关系 |
12. 如图,在△ABC中,AB=AC=2,点D在AC边上,且AD=BD=BC,则cosA的值是( )
如图,在△ABC中,AB=AC=2,点D在AC边上,且AD=BD=BC,则cosA的值是( )
 如图,在△ABC中,AB=AC=2,点D在AC边上,且AD=BD=BC,则cosA的值是( )
如图,在△ABC中,AB=AC=2,点D在AC边上,且AD=BD=BC,则cosA的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{5}+1}{4}$ |
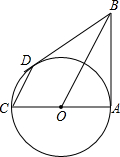 如图,AB与⊙O相切于点A,AC为⊙O的直径,且AC=6,CD∥BO,CD交⊙O于D,连接BD.
如图,AB与⊙O相切于点A,AC为⊙O的直径,且AC=6,CD∥BO,CD交⊙O于D,连接BD.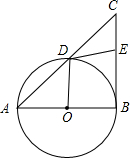 如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC的中点,连接DE、OD.
如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC的中点,连接DE、OD. 如图,直线y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线y=x于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按照此做法进行下去,点B4的纵坐标为2$\sqrt{2}$.
如图,直线y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线y=x于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按照此做法进行下去,点B4的纵坐标为2$\sqrt{2}$.