Question

3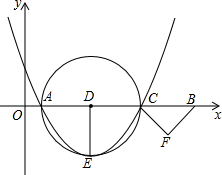．如图，在平面直角坐标系中，点A（1，0）、B（11，0），点C为线段AB上一动点，以AC为直径的⊙D的半径DE⊥AC，△CBF是以CB为斜边的等腰直角三角形，且点E、F都在第四象限，当点F到过点A、C、E三点的抛物线的顶点的距离最小时，该抛物线的解析式为y=$\frac{2}{5}$（x-$\frac{7}{2}$）²-$\frac{5}{2}$．

Answer 1

分析 由⊙D的半径DE⊥AC，△CBF是以CB为斜边的等腰直角三角形，设出点C（m，0），表示出点E（$\frac{m+1}{2}$，$\frac{1-m}{2}$），F（$\frac{m+11}{2}$，$\frac{m-11}{2}$），则有EF²=（m-6）²+36，求出m即可．

解答 解：设点C（m，0），
∵以AC为直径的⊙D的半径DE⊥AC，
∴点E（$\frac{m+1}{2}$，$\frac{1-m}{2}$），
∵△CBF是以CB为斜边的等腰直角三角形，
∴F（$\frac{m+11}{2}$，$\frac{m-11}{2}$），
∴EF²=（$\frac{m-11}{2}-\frac{m+1}{2}$）²+（$\frac{m-11}{2}$-$\frac{1-m}{2}）$²=（m-6）²+36，
当点F到过点A、C、E三点的抛物线的顶点的距离最小，
∴当m=6时，EF_最小=6，
∴C（6，0），E（$\frac{7}{2}$，-$\frac{5}{2}$），
设抛物线的解析式为y=a（x-$\frac{7}{2}$）²-$\frac{5}{2}$，
∵抛物线经过A（1，0），
∴0=a（1-$\frac{7}{2}$）²-$\frac{5}{2}$，
∴a=$\frac{2}{5}$，
∴y=$\frac{2}{5}$（x-$\frac{7}{2}$）²-$\frac{5}{2}$．
故答案为y=$\frac{2}{5}$（x-$\frac{7}{2}$）²-$\frac{5}{2}$．

点评 此题是圆的综合题，主要考查了抛物线的性质，圆的简单性质，解本题的关键是，设出一个量，根据距离最小确定出此量m=6．