题目内容
14.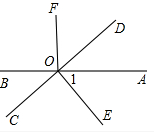 如图,直线AB、CD相交于O,OD平分∠AOF,OE⊥CD于点O,∠1=50°,求∠BOC、∠BOF的度数.
如图,直线AB、CD相交于O,OD平分∠AOF,OE⊥CD于点O,∠1=50°,求∠BOC、∠BOF的度数.解:∵OE⊥CD(已知)
∴∠DOE=90°(垂直的定义)
∵∠1=50°(已知)
∴∠AOD=∠DOE-∠1=40°
∵∠BOC与∠AOD为对顶角(已知)
∴∠BOC=∠AOD=∠40°(对顶角相等)
∵OD平分∠AOF(已知)
且∠AOD=40°(已求)
∴∠AOF=2∠AOD=80°(角平分线定义)
∵∠BOF+∠AOF=180°(邻补角定义)
∴∠BOF=180°-∠AOF=100°.
分析 根据垂直的定义得出∠DOE=90°,那么∠AOD=∠DOE-∠1=40°,利用对顶角相等得出∠BOC=∠AOD=40°;由角平分线定义得出∠AOF=2∠AOD=80°,再根据邻补角定义求出∠BOF=180°-∠AOF=100°.
解答  解:∵OE⊥CD(已知),
解:∵OE⊥CD(已知),
∴∠DOE=90°(垂直的定义),
∵∠1=50°(已知),
∴∠AOD=∠DOE-∠1=40°,
∵∠BOC与∠AOD为对顶角(已知),
∴∠BOC=∠AOD=40°(对顶角相等).
∵OD平分∠AOF(已知),
且∠AOD=40°(已求),
∴∠AOF=2∠AOD=80°(角平分线定义).
∵∠BOF+∠AOF=180°(邻补角定义),
∴∠BOF=180°-∠AOF=100°.
故答案为已知,90,垂直的定义,已知,DOE,1,40,对顶,已知,AOD,40,对顶角相等,已知,40,已求,AOD,80,角平分线定义,180,邻补角定义,180,100.
点评 此题考查了垂线和角平分线的定义,对顶角的性质以及邻补角定义,要注意领会由垂直得直角这一要点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.下面两个数互为相反数的是( )
| A. | -(+9)与+(-9) | B. | -0.5与-(+0.5) | C. | -1.25与$\frac{4}{5}$ | D. | +(-0.01)与-(-$\frac{1}{100}$) |
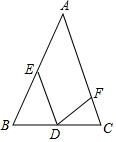 已知:如图,在△ABC中,AB=AC,∠EDF=∠B.求证:△BED∽△CDF.
已知:如图,在△ABC中,AB=AC,∠EDF=∠B.求证:△BED∽△CDF. 如图,平行四边形ABCD中,点E为DC上一点,连接AE,F为AE上一点,连接BF,∠AFB=∠EFB,G在BF上,连接AG、EG,FG平分∠AGE.
如图,平行四边形ABCD中,点E为DC上一点,连接AE,F为AE上一点,连接BF,∠AFB=∠EFB,G在BF上,连接AG、EG,FG平分∠AGE.
 如图,已知平行四边形ABCD中,点E是对角线AC上的一点,且满足AE:EC=1:3,连接BE并延长,交AD于点G,交CD的延长线于点F,求AG:GD的值.
如图,已知平行四边形ABCD中,点E是对角线AC上的一点,且满足AE:EC=1:3,连接BE并延长,交AD于点G,交CD的延长线于点F,求AG:GD的值.