题目内容
6．
如图，已知平行四边形ABCD中，点E是对角线AC上的一点，且满足AE：EC=1：3，连接BE并延长，交AD于点G，交CD的延长线于点F，求AG：GD的值．
分析 由平行四边形ABCD的性质推知AD∥BC，且AD=BC，则易得△AEG∽△CEB，由相似三角形的对应边成比例得到AG：BC的值，继而求得AG：GD的值．
解答 解：∵四边形ABCD是平行四边形，
∴AD∥BC，且AD=BC，
∴△AEG∽△CEB，
∴$\frac{AE}{EC}$=$\frac{AG}{BC}$，即$\frac{1}{3}$=$\frac{AG}{BC}$，
∴$\frac{1}{3}$=$\frac{AG}{AD}$，
∴AG：GD=1：2．
点评 此题考查了平行四边形的性质以及相似三角形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
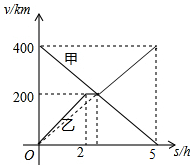甲、乙两辆汽车分别从A、B两地同时出发，沿同一条公路相向而行，乙车出发2h后休息，与甲车相遇后，继续行驶．设甲，乙两车距B地的路程分别为y甲（km），y乙（km），甲车行驶的时间为x（h），y甲，y乙与x之间的函数图象如图所示，结合图象解答下列问题：
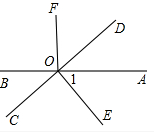如图，直线AB、CD相交于O，OD平分∠AOF，OE⊥CD于点O，∠1=50°，求∠BOC、∠BOF的度数．
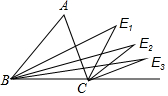如图，∠A=60°，BE1平分∠ABC，CE1平分∠ACD，则∠E1=30°；BE2平分∠E1BC，CE2平分∠E1CD，则∠E2=15°；…；BEn平分∠En-1BC，CEn平分∠En-1CD，则∠En=$\frac{60°}{{2}^{n}}$．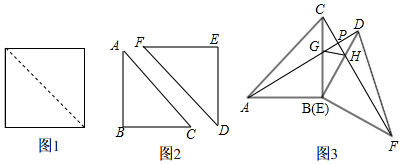
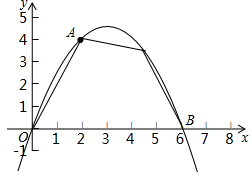如图，二次函数y=ax2+bx的图象经过点A（2，4）与B（6，0）．点C是该二次函数图象上A，B两点之间的一动点，横坐标为x（2＜x＜6），写出四边形OACB的面积S关于点C的横坐标x的函数表达式，并求S的最大值．