题目内容
10.在直角坐标系中,已知点O(0,0),A(1,0),B(1,1),C(2,0),△OBC的面积记为S1,过O、B、C三点的半圆面积记为S2;过O、B、C三点的抛物线与x轴所围成的图形面积记为S3,则S1、S2、S3的大小关系是S2>S3>S1.(用“>”连接)分析 方法一:根据题意画出图象,结合图象即可得;方法二:根据三角形面积公式、圆的面积公式分别求得S1、S2,利用微积分求得S3,比较即可得.
解答 解:方法一,如图所示: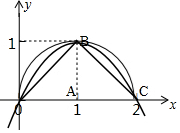
显然S2>S3>S1;
方法二,
由图可知S1=$\frac{1}{2}$•OC•yB=$\frac{1}{2}$×2×1=1,
S2=$\frac{1}{2}$•π•($\frac{OC}{2}$)2=$\frac{1}{2}$•π•1=$\frac{1}{2}$π,
∵抛物线过点O(0,0)、C(2,0)、B(1,1),
∴设抛物线解析式为y=ax(x-2),
将B(1,1)代入,得:-a=1,即a=-1,
∴抛物线解析式为y=-x2+2x,
则S3=${∫}_{0}^{2}$(-x2+2x)=-$\frac{1}{3}$×23+22=$\frac{4}{3}$,
∵$\frac{1}{2}$π>$\frac{4}{3}$>1,
∴S2>S3>S1,
故答案为:S2>S3>S1.
点评 本题主要考查抛物线与x轴的交点,根据题意画出函数图象是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知A(2,y1),B(-3,y2),C(-5,y3)三个点都在反比例函数y=-$\frac{7}{x}$的图象上,比较y1,y2,y3的大小,则下列各式正确的是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y2<y3<y1 | D. | y3<y2<y1 |
15.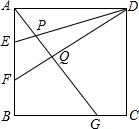 如图,正方形ABCD中,AE=EF=FB,BG=2CG,DE,DF分别交AG于P和Q,以下说法中正确的是( )
如图,正方形ABCD中,AE=EF=FB,BG=2CG,DE,DF分别交AG于P和Q,以下说法中正确的是( )
①AG⊥FD;②AQ:QG=6:7;③EP:PD=2:11;④SGCDQ:SBGQF=17:9.
 如图,正方形ABCD中,AE=EF=FB,BG=2CG,DE,DF分别交AG于P和Q,以下说法中正确的是( )
如图,正方形ABCD中,AE=EF=FB,BG=2CG,DE,DF分别交AG于P和Q,以下说法中正确的是( )①AG⊥FD;②AQ:QG=6:7;③EP:PD=2:11;④SGCDQ:SBGQF=17:9.
| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①②④ |
 如图,将纸片△ABC沿DE折叠,点A落在△ABC的形内,已知∠1+∠2=102°,则∠A的大小等于51度.
如图,将纸片△ABC沿DE折叠,点A落在△ABC的形内,已知∠1+∠2=102°,则∠A的大小等于51度.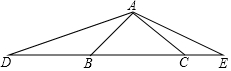 D、E是等腰Rt△ABC斜边BC所在直线上的两点,满足∠DAE=135°.求证:CD2+BE2=DE2.
D、E是等腰Rt△ABC斜边BC所在直线上的两点,满足∠DAE=135°.求证:CD2+BE2=DE2.