题目内容
9.阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作一条线段的垂直平分线.
已知:线段AB.
求作:线段AB的垂直平分线.
小红的作法如下:
如图,①分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径作弧,两弧相交于点C;
②再分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径(不同于①中的半径)作弧,两弧相交于点D,使点D与点C在直线AB的同侧;
③作直线CD.
所以直线CD就是所求作的垂直平分线.
老师说:“小红的作法正确.”
请回答:小红的作图依据是到线段两个端点距离相等的点在这条线段的垂直平分线上;两点确定一条直线.
分析 根据线段垂直平分线的作法即可得出结论.
解答  解:如图,∵由作图可知,AC=BC=AD=BD,
解:如图,∵由作图可知,AC=BC=AD=BD,
∴直线CD就是线段AB的垂直平分线.
故答案为:到线段两个端点距离相等的点在这条线段的垂直平分线上;两点确定一条直线.
点评 本题考查的是作图-基本作图,熟知线段垂直平分线的作法是解答此题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
20.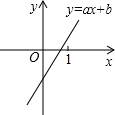 一次函数y=ax+b在直角坐标系中的图象如图所示,则化简$\sqrt{{{(a-b)}^2}}$-|a+b|的结果是( )
一次函数y=ax+b在直角坐标系中的图象如图所示,则化简$\sqrt{{{(a-b)}^2}}$-|a+b|的结果是( )
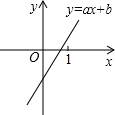 一次函数y=ax+b在直角坐标系中的图象如图所示,则化简$\sqrt{{{(a-b)}^2}}$-|a+b|的结果是( )
一次函数y=ax+b在直角坐标系中的图象如图所示,则化简$\sqrt{{{(a-b)}^2}}$-|a+b|的结果是( )| A. | 2a | B. | -2a | C. | 2b | D. | -2b |
17.-$\sqrt{17}$+1的小数部分是( )
| A. | -$\sqrt{17}$+5 | B. | -$\sqrt{17}$+4 | C. | -$\sqrt{17}$-3 | D. | $\sqrt{17}$-4 |
18.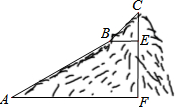 如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,斜坡AB的坡度i=1:2,仰角∠CBE=50°,则山峰的高度CF约为( )米,(可用的参考数据:sin50°≈0.8,tan50°≈1.2,$\sqrt{5}$≈2.24)
如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,斜坡AB的坡度i=1:2,仰角∠CBE=50°,则山峰的高度CF约为( )米,(可用的参考数据:sin50°≈0.8,tan50°≈1.2,$\sqrt{5}$≈2.24)
 如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,斜坡AB的坡度i=1:2,仰角∠CBE=50°,则山峰的高度CF约为( )米,(可用的参考数据:sin50°≈0.8,tan50°≈1.2,$\sqrt{5}$≈2.24)
如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,斜坡AB的坡度i=1:2,仰角∠CBE=50°,则山峰的高度CF约为( )米,(可用的参考数据:sin50°≈0.8,tan50°≈1.2,$\sqrt{5}$≈2.24)| A. | 500 | B. | 516 | C. | 530 | D. | 580 |
19.今年4月29日成都地铁安全运输乘客约181万乘次,又一次刷新客流纪录,这也是今年以来第四次客流纪录的刷新,用科学记数法表示181万为( )
| A. | 18.1×105 | B. | 1.81×106 | C. | 1.81×107 | D. | 181×104 |
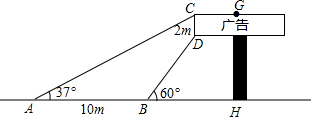 如图,长方形广告牌架在楼房顶部,已知CD=2m,经测量得到∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.(参考数据:tan37°≈0.75,$\sqrt{3}$≈1.732,结果精确到0.1m)
如图,长方形广告牌架在楼房顶部,已知CD=2m,经测量得到∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.(参考数据:tan37°≈0.75,$\sqrt{3}$≈1.732,结果精确到0.1m)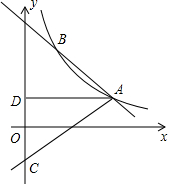 如图,反比例函数y=$\frac{k}{x}$(x>0)图象经过点A(2$\sqrt{3}$,1),直线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
如图,反比例函数y=$\frac{k}{x}$(x>0)图象经过点A(2$\sqrt{3}$,1),直线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.