题目内容
3.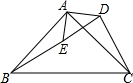 如图,△ABC是等腰直角三角形,∠BAC=90°,△ADC绕点A旋转,使得边AC与AB重合,点D与点E重合,若AD=3,则DE=3$\sqrt{2}$.
如图,△ABC是等腰直角三角形,∠BAC=90°,△ADC绕点A旋转,使得边AC与AB重合,点D与点E重合,若AD=3,则DE=3$\sqrt{2}$.
分析 根据旋转的定义,利用点D与点E重合,AB=AC,∠BAC=90°,可判断△ABD绕A点逆时针旋转90°得到△ACE,于是可根据旋转的性质得△ABD≌△ACE,AD=AE=3,∠DAE=90°,接着判断△ADE为等腰直角三角形,然后根据等腰直角三角形的性质计算DE的长.
解答 解: ∵△ABD绕点A逆时针旋转90°,点D与点E重合,
∵△ABD绕点A逆时针旋转90°,点D与点E重合,
而AB=AC,∠BAC=90°,
∴△ABD绕A点逆时针旋转90°得到△ACE,
∴△ABD≌△ACE;AD=AE=3,∠DAE=90°,
∴△ADE为等腰直角三角形,
∴DE=$\sqrt{2}$AD=3$\sqrt{2}$.
故答案为:3$\sqrt{2}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的判定与性质.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
9.下列运算正确的是( )
| A. | (a+b)2=a2+b2 | B. | a(a+b)=a2+ab | C. | -2(a-1)=-2a-2 | D. | 3a2-2a2=1 |
12.在用配方法解下列方程时,配方有错误的是( )
| A. | x2-2x-99=0⇒(x-1)2=100 | B. | 2t2-7t-4=0⇒${(t-\frac{7}{4})^2}=\frac{81}{8}$ | ||
| C. | x2+8x-9=0⇒(x+4)2=25 | D. | y2-4y=2⇒( y-2 )2=6 |