题目内容
12.在用配方法解下列方程时,配方有错误的是( )| A. | x2-2x-99=0⇒(x-1)2=100 | B. | 2t2-7t-4=0⇒${(t-\frac{7}{4})^2}=\frac{81}{8}$ | ||
| C. | x2+8x-9=0⇒(x+4)2=25 | D. | y2-4y=2⇒( y-2 )2=6 |
分析 配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
解答 解:B、由已知方程得到:x2-2x+1-99-1=0,则(x-1)2=100,故本选项错误;
B、由已知方程得到:t2-$\frac{7}{2}$t+($\frac{7}{4}$)2-2-($\frac{7}{4}$)2=0,所以(t-$\frac{7}{4}$)2=$\frac{81}{16}$,故本选项正确;
C、由已知方程得到:x2+8x+16-9-16=0,所以(x+4)2=25,故本选项错误;
D、由已知方程得到:y2-4y+4=2+4,所以(y-2)2=6,故本选项错误.
故选:B.
点评 此题考查了配方法解一元二次方程,解题时要注意解题步骤的准确应用.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
相关题目
18.下列计算中正确的是( )
| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | B. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | C. | (a+b)2=a2+b2 | D. | a2•a3=a6 |
20.当x=1时,代数式ax3+bx+1的值是2,则方程$\frac{ax+1}{2}$+$\frac{2bx-3}{4}$=$\frac{x}{4}$的解是( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 1 | D. | -1 |
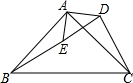 如图,△ABC是等腰直角三角形,∠BAC=90°,△ADC绕点A旋转,使得边AC与AB重合,点D与点E重合,若AD=3,则DE=3$\sqrt{2}$.
如图,△ABC是等腰直角三角形,∠BAC=90°,△ADC绕点A旋转,使得边AC与AB重合,点D与点E重合,若AD=3,则DE=3$\sqrt{2}$.