题目内容
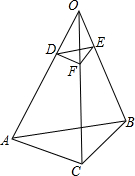 如图所示,如果D、E、F分别在OA、OB、OC上,且DF∥AC,EF∥BC.求证:
如图所示,如果D、E、F分别在OA、OB、OC上,且DF∥AC,EF∥BC.求证:(1)OD:OA=OE:OB;
(2)△ODE∽△OAB;
(3)△ABC∽△DEF.
考点:相似三角形的判定与性质
专题:证明题
分析:(1)根据平行于三角形一边的直线截其他两边所得的新三角形与原三角形相似就可以得出结论;
(2)根据OD:OA=OE:OB由∠AOB=∠AOB就可以得出△ODE∽△OAB;
(3)由△ODE∽△OAB就可以得出
=
=
就可以得出结论.
(2)根据OD:OA=OE:OB由∠AOB=∠AOB就可以得出△ODE∽△OAB;
(3)由△ODE∽△OAB就可以得出
| DE |
| AB |
| DF |
| AC |
| EF |
| CB |
解答:证明:(1)∵DF∥AC,EF∥BC,
∴△ODF∽△OAC,△OEF∽△OBC,
∴
=
=
,
=
=
,
∴OD:OA=OE:OB;
(2)∵OD:OA=OE:OB,∠DOE=∠AOB,
∴△ODE∽△OAB.
(3)∵△ODE∽△OAB,
∴
=
=
,
∴
=
=
.
∴△ABC∽△DEF.
∴△ODF∽△OAC,△OEF∽△OBC,
∴
| OD |
| OA |
| OF |
| OC |
| DF |
| AC |
| OF |
| OC |
| OE |
| OB |
| EF |
| BC |
∴OD:OA=OE:OB;
(2)∵OD:OA=OE:OB,∠DOE=∠AOB,
∴△ODE∽△OAB.
(3)∵△ODE∽△OAB,
∴
| OD |
| OA |
| OE |
| OB |
| DE |
| AB |
∴
| DE |
| AB |
| DF |
| AC |
| EF |
| CB |
∴△ABC∽△DEF.
点评:本题考查了平行于三角形一边的直线截其他两边所得的新三角形与原三角形相似的判定方法的运用,相似三角形的性质的运用,相似三角形的判定的运用,解答时证明三角形相似是关键.

练习册系列答案
相关题目
 如图,E,F在BC上,BE=CF,AB=CD,AB∥CD.求证:
如图,E,F在BC上,BE=CF,AB=CD,AB∥CD.求证: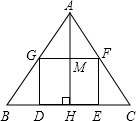 如图,已知△ABC,矩形GDEF的DE边在BC边上,G,F分别在AB,AC边上,BC=5cm,S△ABC=30cm2,AB为△ABC在BC边上的高,求△ABC的内接长方形GDEF的最大面积.
如图,已知△ABC,矩形GDEF的DE边在BC边上,G,F分别在AB,AC边上,BC=5cm,S△ABC=30cm2,AB为△ABC在BC边上的高,求△ABC的内接长方形GDEF的最大面积.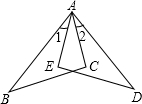 如图,已知AB=AD,AC=AE,∠1=∠2,求证:BC=DE.
如图,已知AB=AD,AC=AE,∠1=∠2,求证:BC=DE.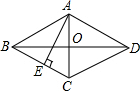 在菱形ABCD中,AE垂直平分BC,垂足为E,AB=4cm,求菱形的面积和对角线BD的长.
在菱形ABCD中,AE垂直平分BC,垂足为E,AB=4cm,求菱形的面积和对角线BD的长.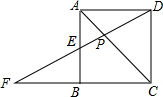 如图,正方形ABCD中,F是CB延长线上的一点,DF交AB于E,交对角线AC于P,如PE=2,EF=3.求PD的长.
如图,正方形ABCD中,F是CB延长线上的一点,DF交AB于E,交对角线AC于P,如PE=2,EF=3.求PD的长. 如图,在边长为2的正△ABC中,点E为线段BC的中点,点P为线段AC上的动点,在BP绕点B顺时针方向旋转过程中,点P的对应点为P1,设EP1=t,则t的范围是
如图,在边长为2的正△ABC中,点E为线段BC的中点,点P为线段AC上的动点,在BP绕点B顺时针方向旋转过程中,点P的对应点为P1,设EP1=t,则t的范围是