题目内容
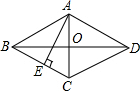 在菱形ABCD中,AE垂直平分BC,垂足为E,AB=4cm,求菱形的面积和对角线BD的长.
在菱形ABCD中,AE垂直平分BC,垂足为E,AB=4cm,求菱形的面积和对角线BD的长.考点:菱形的性质
专题:
分析:根据线段垂直平分线上的点到两端点的距离相等可得AB=AC,然后判断出△ABC是等边三角形,再根据等边三角形的性质求出AE,然后利用菱形的面积公式列式计算即可得解;再根据菱形的面积等于对角线乘积的一半列式求解即可得到BD.
解答:解:∵AE垂直平分BC,
∴AB=AC,
又∵菱形ABCD的边AB=BC,
∴△ABC是等边三角形,
∴AE=
AB=
×4=2
cm,
∴菱形的面积=4×2
=8
cm2;
又菱形的面积=
AC•BD=
×4•BD=2BD,
∴2BD=8
,
解得BD=4
cm.
∴AB=AC,
又∵菱形ABCD的边AB=BC,
∴△ABC是等边三角形,
∴AE=
| ||
| 2 |
| ||
| 2 |
| 3 |
∴菱形的面积=4×2
| 3 |
| 3 |
又菱形的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∴2BD=8
| 3 |
解得BD=4
| 3 |
点评:本题考查了菱形的性质,线段垂直平分线上的点到两端点的距离相等的性质,等边三角形的判定与性质,判断出△ABC是等边三角形是解题的关键.

练习册系列答案
相关题目
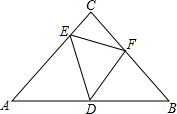 如图,已知Rt△ABC中,AC=BC,∠C=90°,D、E、F分别在AB、AC、BC边上,∠EDF=45°.
如图,已知Rt△ABC中,AC=BC,∠C=90°,D、E、F分别在AB、AC、BC边上,∠EDF=45°. 如图,用三个全等的等边三角形纸片,将它们拼成一个与等腰梯形全等的图案,可以怎样拼?在梯形中画出来.
如图,用三个全等的等边三角形纸片,将它们拼成一个与等腰梯形全等的图案,可以怎样拼?在梯形中画出来. 把图中的各图补画成以l为对称轴的轴对称图形.
把图中的各图补画成以l为对称轴的轴对称图形.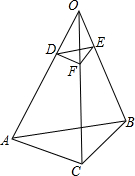 如图所示,如果D、E、F分别在OA、OB、OC上,且DF∥AC,EF∥BC.求证:
如图所示,如果D、E、F分别在OA、OB、OC上,且DF∥AC,EF∥BC.求证:
 如图,在Rt△ABC中,AC=8,BC=6,∠C=90°.⊙I分别切AC,BC,AB于点D,E,F,求Rt△ABC的内心I与外心O之间的距离.
如图,在Rt△ABC中,AC=8,BC=6,∠C=90°.⊙I分别切AC,BC,AB于点D,E,F,求Rt△ABC的内心I与外心O之间的距离. 如图,四边形ABCD∽四边形A′B′C′D′,则CD=
如图,四边形ABCD∽四边形A′B′C′D′,则CD=