题目内容
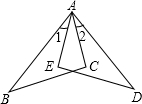如图，已知AB=AD，AC=AE，∠1=∠2，求证：BC=DE．考点：全等三角形的判定与性质
专题：证明题
分析：由∠1=∠2根据等式的性质就可以得出∠BAC=∠DAE就可以得出△BAC≌△DAE，就可以得出结论．
解答：证明：∵∠1=∠2，
∴∠1+∠EAC=∠2+∠EAC，
∴∠BAC=∠DAE．
在△BAC和△DAE中，
，
∴△BAC≌△DAE（SAS），
∴BC=DE．
∴∠1+∠EAC=∠2+∠EAC，
∴∠BAC=∠DAE．
在△BAC和△DAE中，
|
∴△BAC≌△DAE（SAS），
∴BC=DE．
点评：本题考查了等式的性质的运用，全等三角形的判定及性质的运用，证明三角形全等是关键．
练习册系列答案
精英口算卡系列答案
相关题目
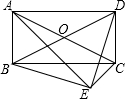如图，在平行四边形ABCD中，以AC为斜边作Rt△ACE，且∠BED是直角．求证：平行四边形ABCD是矩形．
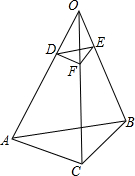如图所示，如果D、E、F分别在OA、OB、OC上，且DF∥AC，EF∥BC．求证：
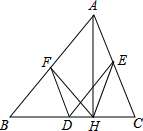如图，在△ABC中，D，E，F分别为BC，AC，AB的中点．若AH⊥BC于点H，∠BAC=60°，则∠FDE=