题目内容
3.如图1是由边长为1的小正方形组成的网格,点A、B、C、D都在网格的格点上,AC、BD相交于点O.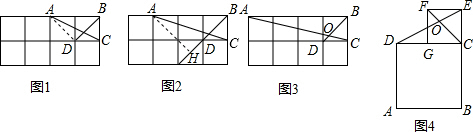
(一)探索发现
(1)如图1,当AB=2时,连接AD,则∠ADO=90°,BO=2DO,AD=$\sqrt{2}$,BO=$\frac{2}{3}$ $\sqrt{2}$,tan∠AOD=3.
如图2,当AB=3时,画AH⊥BD交BD的延长线于H,则AH=$\frac{3}{2}$ $\sqrt{2}$,
BO=$\frac{3}{4}$$\sqrt{2}$,tan∠AOD=2.
如图3,当AB=4时,tan∠AOD=$\frac{5}{3}$.
(2)猜想:当AB=n (n>0)时,tan∠AOD=$\frac{n+1}{n-1}$.(结果用含n的代数式表示),请证明你的猜想.
(二)解决问题
(3)如图,两个正方形的一边CD、CG在同一直线上,连接CF、DE相交于点O,若tan∠COE=$\frac{17}{13}$,求正方形ABCD和正方形CEFG的边长之比.
分析 (1)设四边形DCBE为正方形,连接CE,交BD于F,先由正方形的性质得出CF=DF=BF,BD⊥CE,再由AB∥DC,得△AOB∽△COD,根据相似三角形的对应边成比例得DO:BO=CD:AB,即可得OF:CF的值,然后在Rt△OCF中,求得tan∠COF的值,即为tan∠AOD的值;根据S△ABD=$\frac{1}{2}$BD•AH=$\frac{1}{2}$AB•ED,即可求出AH;
(2)当AB=n(n>0)时,tan∠AOD=$\frac{n+1}{n-1}$,同(1)证明即可;
(3)设正方形ABCD与正方形CEFG的边长之比为k,由(2)的结论得到$\frac{n+1}{n-1}$=$\frac{17}{13}$,解方程即可.
解答  解:(一)探索发现
解:(一)探索发现
(1)如图1,当AB=2时,∵BO=2DO,BO=$\frac{2}{3}$ $\sqrt{2}$,
∴OD=$\frac{\sqrt{2}}{3}$,
又∵∠ADO=90°,AD=$\sqrt{2}$,
∴tan∠AOD=$\frac{AD}{OD}$=$\frac{\sqrt{2}}{\frac{\sqrt{2}}{3}}$=3,
即tan∠AOD=3.
如图2,设DCBE为正方形,连接CE,交BD于F.
∵四边形BCDE是正方形,
∴DF=CF=BF=$\frac{1}{2}$BD=$\frac{1}{2}$CE,BD⊥CE.
根据题意得:AB∥DC,
∴△AOB∽△COD,
∴DO:BO=CD:AB.
当AB=3时,DO:BO=1:3,
∴BO=$\frac{3\sqrt{2}}{4}$.
∵S△ABD=$\frac{1}{2}$BD•AH=$\frac{1}{2}$AB•ED,
∴BD•AH=AB•ED,
∴AH=$\frac{AB•ED}{BD}$=$\frac{3×1}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$,
DO:BO=CD:AB=1:3,
∴DO:DF=1:2,
∴OF:DF=1:2,即OF:CF=1:2.
在Rt△OCF中,tan∠COF=$\frac{CF}{OF}$=2,
∵∠AOD=∠COF,
∴tan∠AOD=2;
如图3,当AB=4时,DO:BO=CD:AB=1:4,
∴DO:DF=1:2.5=2:5,
∴OF:DF=3:5,即OF:CF=3:5.
在Rt△OCF中,tan∠COF=$\frac{CF}{OF}$=$\frac{5}{3}$,
∵∠AOD=∠COF,
∴tan∠AOD=$\frac{5}{3}$;
故答案是:3;$\frac{3}{4}$$\sqrt{2}$;2;$\frac{5}{3}$;
(2)猜想:当AB=n(n>0)时,tan∠AOD=$\frac{n+1}{n-1}$(结果用含n的代数式表示).
证明:过点A作AH⊥BH于点H,则AH=BH=$\frac{\sqrt{2}}{2}$n.
∵AB∥OD,
∴△AOB∽△COD,
∴$\frac{OB}{OD}$=$\frac{AB}{CD}$=$\frac{n}{1}$,
∴OB=$\frac{\sqrt{2}n}{n+1}$.
∴OH=BH-OB=$\frac{\sqrt{2}}{2}$n-$\frac{\sqrt{2}n}{n+1}$.
∴tan∠AOD=$\frac{AH}{HD}$=$\frac{\frac{\sqrt{2}}{2}n}{\frac{\sqrt{2}}{2}n-\frac{\sqrt{2}n}{n+1}}$=$\frac{n+1}{n-1}$;
故答案是:$\frac{n+1}{n-1}$;
(二)解决问题
(3)解:如图4,过点D作DH⊥CF于点H,则tan∠DOH=$\frac{DH}{HO}$.
∵∠DOH=∠COE,
∴tan∠DOH=$\frac{17}{13}$,
又由(一)结论得:$\frac{n+1}{n-1}$=$\frac{17}{13}$,
∴n=$\frac{15}{2}$
∴正方形ABCD和正方形CEFG的边长之比为 $\frac{15}{2}$.
点评 此题考查了正方形的性质,相似三角形的判定与性质,三角函数的定义,三角形的面积.此题难度适中,解题的关键是准确作出辅助线,注意转化思想与数形结合思想的应用.

 阅读快车系列答案
阅读快车系列答案 如图,AB为⊙O的直径,C、D是⊙O上的两点,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E的度数为( )
如图,AB为⊙O的直径,C、D是⊙O上的两点,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E的度数为( )| A. | 40° | B. | 50° | C. | 55° | D. | 60° |
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
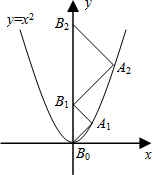 如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形(点B0是坐标原点),则△A2015B2014B2015的腰长=2015$\sqrt{2}$.
如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形(点B0是坐标原点),则△A2015B2014B2015的腰长=2015$\sqrt{2}$. 如图所示,直线AB,CD相交于点O,OE平分∠AOC,若∠AOD-∠DOB=50°,则∠EOB=147.5°.
如图所示,直线AB,CD相交于点O,OE平分∠AOC,若∠AOD-∠DOB=50°,则∠EOB=147.5°.