题目内容
17. 如图,AB为⊙O的直径,C、D是⊙O上的两点,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E的度数为( )
如图,AB为⊙O的直径,C、D是⊙O上的两点,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E的度数为( )| A. | 40° | B. | 50° | C. | 55° | D. | 60° |
分析 首先连接OC,由切线的性质可得OC⊥CE,又由圆周角定理,可求得∠COB的度数,继而可求得答案.
解答  解:连接OC,
解:连接OC,
∵CE是⊙O的切线,
∴OC⊥CE,
即∠OCE=90°,
∵∠COB=2∠CDB=50°,
∴∠E=90°-∠COB=40°.
故选A.
点评 本题考查了切线性质,三角形的外角性质,圆周角定理,等腰三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
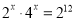 ,则
,则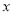 的值为( )
的值为( ) 如图,四边形ABCD为正方形,P为正方形ABCD外一点△ABP经过旋转后到达△BCQ的位置,那么旋转中心是B,旋转角是90度.
如图,四边形ABCD为正方形,P为正方形ABCD外一点△ABP经过旋转后到达△BCQ的位置,那么旋转中心是B,旋转角是90度.