题目内容
20.⊙O1、⊙O2的半径分别为4和5,线段O1O2的长为3,则两圆的位置关系为相交.分析 由两圆的半径分别为4和5,圆心距为3,易得圆心距大于两半径之差、小于两半径之和,根据两圆的位置关系的判定方法即可得到它们的位置关系为相交.
解答 解:∵两圆的半径分别为4和5,圆心距为3,
∴5-4<d<5+4,
∴两圆相交,
故答案为:相交.
点评 本题考查了两圆的位置关系,牢记圆心距d与两圆的半径之间的关系是解答本题的关键,注意:两圆的位置关系:设两圆半径分别为R、r,两圆圆心距为d,则d>R+r?两圆外离;d=R+r?两圆外切;R-r<d<R+r(R≥r)?两圆相交;d=R-r(R>r)?两圆内切;0≤d<R-r(R>r)?两圆内含.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
12.若函数y=k1x(k1≠0)和函数y=$\frac{{k}_{2}}{x}$(k2≠0)在同一坐标系内的图象没有公共点,则k1和k2( )
| A. | 互为倒数 | B. | 符号相同 | C. | 绝对值相等 | D. | 符号相反 |
8.以下列各组数据为长度三条线段,能组成三角形的是( )
| A. | 5、3、9 | B. | 5、3、7 | C. | 5、3、8 | D. | 6、4、2 |
 如图,四边形ABCD为正方形,P为正方形ABCD外一点△ABP经过旋转后到达△BCQ的位置,那么旋转中心是B,旋转角是90度.
如图,四边形ABCD为正方形,P为正方形ABCD外一点△ABP经过旋转后到达△BCQ的位置,那么旋转中心是B,旋转角是90度.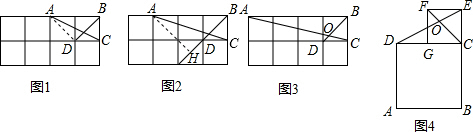
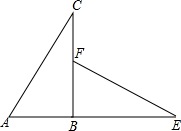 如图,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF,△ABC旋转后能与△FBE重合,请回答:
如图,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF,△ABC旋转后能与△FBE重合,请回答: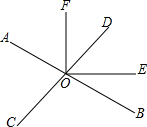 如图,两直线AB、CD相交于点O,OE平分∠BOD,如果∠AOC:∠AOD=7:11
如图,两直线AB、CD相交于点O,OE平分∠BOD,如果∠AOC:∠AOD=7:11