题目内容
9．一个多边形的内角和是它的外角和的3倍，则这个多边形的边数为八．分析 根据多边形的内角和定理，多边形的内角和等于（n-2）•180°，外角和等于360°，然后列方程求解即可．
解答 解：设多边形的边数是n，根据题意得，
（n-2）•180°=3×360°，
解得n=8，
∴这个多边形为八边形．
故答案为：八．
点评 本题主要考查了多边形的内角和公式与外角和定理，根据题意列出方程是解题的关键，要注意“八”不能用阿拉伯数字写．
练习册系列答案
相关题目
2．
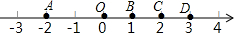如图，已知数轴上的点A，O，B，C，D分别表示数-2，0，1，2，3，则表示数2-$\sqrt{2}$的点P应落在线段（ ）
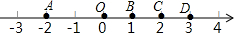如图，已知数轴上的点A，O，B，C，D分别表示数-2，0，1，2，3，则表示数2-$\sqrt{2}$的点P应落在线段（ ）| A． | AO上 | B． | OB上 | C． | BC上 | D． | CD上 |
17．若一元二次方程x2-2x-2015=0的两根为a，b，则a2-3a-b的值为（ ）
| A． | 2012 | B． | 2013 | C． | 2014 | D． | 2015 |
4．下列根式中是最简二次根式的是（ ）
| A． | $\sqrt{{a}^{2}+1}$ | B． | $\sqrt{\frac{1}{2}}$ | C． | $\sqrt{8}$ | D． | $\sqrt{0.1}$ |
14．下列语句，是真命题的是（ ）
| A． | 对顶角相等 | B． | 同位角相等 | C． | 内错角相等 | D． | 同旁内角互补 |
19．已知反比例函数的图象经过点P（a，a），则这个函数的图象位于（ ）
| A． | 第一、三象限 | B． | 第二、三象限 | C． | 第二、四象限 | D． | 第三、四象限 |