题目内容
14. 如图所示,是某公司一电热淋浴器水箱的水量y(升)与供水时间x(分)的函数关系.
如图所示,是某公司一电热淋浴器水箱的水量y(升)与供水时间x(分)的函数关系.(1)求y与x的函数关系式;
(2)求:在30min时水箱里有多少升水?
分析 (1)根据图象可设y与x的函数关系式为:y=kx+b,利用待定系数法就可求得解析式.
(2)把x=30代入函数解析式求值即可.
解答 解:(1)根据图象可设y与x的函数关系式为:y=kx+b,
把点(10,50),(50,150)代入得,$\left\{\begin{array}{l}{10k+b=50}\\{50k+b=150}\end{array}\right.$
解得:k=$\frac{5}{2}$,b=25,
∴y=$\frac{5}{2}$x+25;
(2)当x=30时,y=$\frac{5}{2}$×30+25=100.即求在30分钟时水箱有100升水.
点评 主要考查利用一次函数的模型解决实际问题的能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义准确的列出解析式,再把对应值代入求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.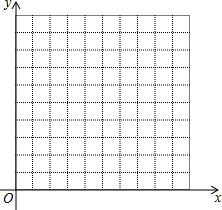 在平面直角坐标系中,点A从原点O出发,每次向上移动2个单位长度或向右移动1个单位长度.
在平面直角坐标系中,点A从原点O出发,每次向上移动2个单位长度或向右移动1个单位长度.
(1)实验操作:
在平面直角坐标系中描出点A从点O出发,移动1次后,2次后,3次后可能到达的点,并把相应点的坐标填写在表格中:
(2)观察发现:
任一次移动,点A可能到达的点在我们学过的一种函数的图象上,
①求移动1次后点A可能到达的点所在图象的函数表达式;
②移动2次后在函数y=-2x+4的图象上,…由此我们知道,移动n次后在函数y=-2x+2n的图象上.(请填写相应的函数表达式)
(3)探索运用:
点A从点O出发经过n次移动后,到达直线y=x上的点B,且平移的总路径长为20,求点B的坐标.
 在平面直角坐标系中,点A从原点O出发,每次向上移动2个单位长度或向右移动1个单位长度.
在平面直角坐标系中,点A从原点O出发,每次向上移动2个单位长度或向右移动1个单位长度.(1)实验操作:
在平面直角坐标系中描出点A从点O出发,移动1次后,2次后,3次后可能到达的点,并把相应点的坐标填写在表格中:
| A从点O出发移动次数 | 可能到达的点的坐标 |
| 1次 | (0,2),(1,0) |
| 2次 | (0,4),(1,2),(2,0) |
| 3次 | (0,6),(1,4),(2,2),(3,0) |
任一次移动,点A可能到达的点在我们学过的一种函数的图象上,
①求移动1次后点A可能到达的点所在图象的函数表达式;
②移动2次后在函数y=-2x+4的图象上,…由此我们知道,移动n次后在函数y=-2x+2n的图象上.(请填写相应的函数表达式)
(3)探索运用:
点A从点O出发经过n次移动后,到达直线y=x上的点B,且平移的总路径长为20,求点B的坐标.
6.阅读材料:在△ABC中,有一点P,当P1、A、B、C没有任何三点在同一直线上,可构成三个不重叠的小三角形(如图).当△ABC内的点的个数增加时,若其它条件不变,三角形内互补重叠的小三角形的个数情况怎样?请观察图形和表格填空.表格中的空白处应填( )

| △ABC内点的个数 | 1 | 2 | 3 | … | 12 |
| 构成不重叠的小三角形的个数 | 3 | 5 | 7 | … |

| A. | 21 | B. | 23 | C. | 25 | D. | 28 |
3.一桶纯净水(含桶)重P千克,桶本身重1千克,将水平均分成4份,则每份水重( )
| A. | $\frac{P}{4}$千克 | B. | $\frac{P-1}{4}$千克 | C. | ($\frac{P}{4}$-1)千克 | D. | $\frac{P+1}{4}$千克 |
4. 二次函数y=-x2+bx+c的大致图象如图所示,则下列结论不成立的是( )
二次函数y=-x2+bx+c的大致图象如图所示,则下列结论不成立的是( )
 二次函数y=-x2+bx+c的大致图象如图所示,则下列结论不成立的是( )
二次函数y=-x2+bx+c的大致图象如图所示,则下列结论不成立的是( )| A. | c=0 | B. | -1-b+c>0 | C. | -2<b<0 | D. | b>0 |
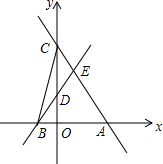 直线y=-$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点C,过点B(-1,0)的直线交线段OC于点D,交线段AC于点E,连接BC,△CDB的面积为1.
直线y=-$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点C,过点B(-1,0)的直线交线段OC于点D,交线段AC于点E,连接BC,△CDB的面积为1.