题目内容
17.已知x=3+2$\sqrt{2}$,y=3-2$\sqrt{2}$,求下列代数式的值.(1)x2-3xy+y2
(2)$\frac{y}{x}+\frac{x}{y}-4$.
分析 (1)把所求的式子化成(x-y)2-xy的形式,然后代入求解求解;
(2)把所求的式子化成 $\frac{{x}^{2}+{y}^{2}-4xy}{xy}$=$\frac{(x-y)^{2}-2xy}{xy}$=$\frac{(x-y)^{2}}{xy}$-2形式,然后代入求解求解.
解答 解:(1)原式=(x-y)2-xy
知x=3+2$\sqrt{2}$,y=3-2$\sqrt{2}$,则x=3+2$\sqrt{2}$,y=3-2$\sqrt{2}$时,原式=(4$\sqrt{2}$)2-(3+2$\sqrt{2}$)(3-2$\sqrt{2}$)=32-(9-8)=32-1=31;
(2)原式=$\frac{{x}^{2}+{y}^{2}-4xy}{xy}$=$\frac{(x-y)^{2}-2xy}{xy}$=$\frac{(x-y)^{2}}{xy}$-2,
当x=3+2$\sqrt{2}$,y=3-2$\sqrt{2}$时,原式=$\frac{(4\sqrt{2})^{2}}{(3+2\sqrt{2})(3-2\sqrt{2})}$-2=$\frac{32}{9-8}$-2=32-2=30.
点评 本题考查了二次根式的化简求值,正确理解平方差公式的结构,正确对所求的式子进行变形是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.已知点A(x1,y1),B(x2,y2)、C(x3,y3)在抛物线y=x2+2x+m的图象上,若x1<x2<-1<x3,且|x3+1|>|x1+1|,那么y1,y2,y3的大小关系( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y1>y2 | D. | y2>y1>y3 |
5.下列式子正确的是( )
| A. | -52=(-5)×(-5) | B. | 32=3×2 | C. | 32=3+3 | D. | -(-$\frac{1}{2}$)2=-$\frac{1}{2}$×$\frac{1}{2}$ |
7. 如图,直线AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的大小为( )
如图,直线AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的大小为( )
 如图,直线AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的大小为( )
如图,直线AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的大小为( )| A. | 35° | B. | 40° | C. | 50° | D. | 65° |
 如图,△ABC,按要求完成下列各题:
如图,△ABC,按要求完成下列各题:



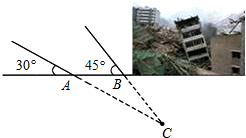 一方有难八方支援.安徽地震局救援队在某次地震救援中,探测出某建筑物废墟下方点C处有生命迹象,在废墟一侧某面上选两探测点A、B,AB相距2.1米,探测线与地面的夹角分别是35°和45°(如图),试确定生命所在点C与探测面的距离(参考数据$\sqrt{2}$≈1.4,≈1.7)
一方有难八方支援.安徽地震局救援队在某次地震救援中,探测出某建筑物废墟下方点C处有生命迹象,在废墟一侧某面上选两探测点A、B,AB相距2.1米,探测线与地面的夹角分别是35°和45°(如图),试确定生命所在点C与探测面的距离(参考数据$\sqrt{2}$≈1.4,≈1.7)