题目内容
1．已知：a、b、c是三角形ABC的三边，化简：|a-b-c|+|a+b-c|结果是（ ）| A． | 2a-2c | B． | 2b | C． | 2a | D． | 2b-2a |
分析 根据三角形三边满足的条件是，两边和大于第三边，两边的差小于第三边，根据此来确定绝对值内的式子的正负，从而化简计算即可．
解答 解：∵a、b、c是三角形的三边长，
∴a+b-c＞0，a-b-c＜0，
∴原式=-（a-b-c）+a+b-c=-a+b+c+a+b-c=2b，
故选B．
点评 本题考查的是三角形的三边关系，熟知三角形任意两边之和大于第三边，任意两边之差小于第三边是解答此题的关键．
练习册系列答案
相关题目
16．
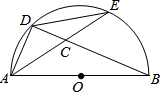如图所示，AB是⊙O的直径，D、E是半圆上任意两点，连接AD、DE，AE与BD相交于点C，要是△ADC与△ABD相似，可以添加一个条件．下列添加的条件中错误的是（ ）
如图所示，AB是⊙O的直径，D、E是半圆上任意两点，连接AD、DE，AE与BD相交于点C，要是△ADC与△ABD相似，可以添加一个条件．下列添加的条件中错误的是（ ）| A． | ∠ACD=∠DAB | B． | AD=DE | C． | AD•AB=CD•BD | D． | AD2=BD•CD |
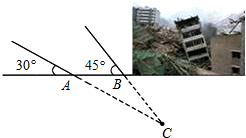一方有难八方支援．安徽地震局救援队在某次地震救援中，探测出某建筑物废墟下方点C处有生命迹象，在废墟一侧某面上选两探测点A、B，AB相距2.1米，探测线与地面的夹角分别是35°和45°（如图），试确定生命所在点C与探测面的距离（参考数据$\sqrt{2}$≈1.4，≈1.7）
13．不等式x-4＜0的正整数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 无数多个 |