题目内容
11.化简并求值:$\frac{x-y}{{{x^2}-2xy+{y^2}}}-\frac{{xy+{y^2}}}{{{x^2}-{y^2}}}$,其中(x+2)2+|y-3|=0.分析 根据绝对值和偶次方的性质求出x,y的值,再把分式的值化到最简,代值计算即可.
解答 解:∵(x+2)2+|y-3|=0,
∴x=-2,y=3,
∴$\frac{x-y}{{{x^2}-2xy+{y^2}}}-\frac{{xy+{y^2}}}{{{x^2}-{y^2}}}$=$\frac{x-y}{(x-y)^{2}}$-$\frac{y(x+y)}{(x+y)(x-y)}$=$\frac{1-y}{x-y}$,
把x=-2,y=3代入上式得;
原式=$\frac{1-3}{-2-3}$=$\frac{2}{5}$.
点评 此题考查了分式的化简求值,用到的知识点是非负数的性质、平方差公式和完全平方公式,关键是根据公式把分式的值化到最简再代值.

练习册系列答案
相关题目
3.小红的妈妈买来30个果冻布丁,分给小红和她的弟弟,小红得到的果冻布丁的数量比她弟弟的2倍少6个,若小红的弟弟得到x个,则可列方程为( )
| A. | 2x-6+x=30 | B. | x+6+2x=30 | C. | $\frac{1}{2}$x+6+x=30 | D. | $\frac{1}{2}$x+6+x=30 |
 如图,抛物线y=ax2+bx-3经过A(1,0),B(3,0)两点.
如图,抛物线y=ax2+bx-3经过A(1,0),B(3,0)两点.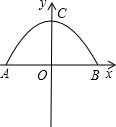 如图,拱桥呈抛物线形,其函数关系式为y=-$\frac{1}{4}$x2+h,当拱桥下水位线在AB位置时,水面宽为12米:
如图,拱桥呈抛物线形,其函数关系式为y=-$\frac{1}{4}$x2+h,当拱桥下水位线在AB位置时,水面宽为12米: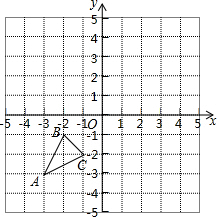 如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是直角坐标平面上三点.
如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是直角坐标平面上三点. 在某月的日历上用正方形圈到a、b、c、d四个数(如图),如果d=18,那么a+b+c=38.
在某月的日历上用正方形圈到a、b、c、d四个数(如图),如果d=18,那么a+b+c=38.