题目内容
2．菱形的两条对角线长分别为6和8，则这个菱形的边长为5．分析 首先根据题意画出图形，由菱形ABCD中，AC=6，BD=8，即可得AC⊥BD，OA=$\frac{1}{2}$AC=3，OB=$\frac{1}{2}$BD=4，然后利用勾股定理求得这个菱形的边长．
解答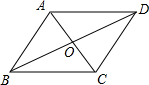 
解：∵菱形ABCD中，AC=6，BD=8，
∴AC⊥BD，OA=$\frac{1}{2}$AC=3，OB=$\frac{1}{2}$BD=4，
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5．
即这个菱形的边长为：5．
故答案为：5．
点评 此题考查了菱形的性质以及勾股定理．注意菱形的对角线互相平分且垂直．
练习册系列答案
相关题目
13．
如图，△ABC中，E为边BC延长线上一点，∠ABC的平分线与∠ACE的平分线交于点D，若∠A=46°，则∠D的度数为（ ）
如图，△ABC中，E为边BC延长线上一点，∠ABC的平分线与∠ACE的平分线交于点D，若∠A=46°，则∠D的度数为（ ）| A． | 46° | B． | 92° | C． | 44° | D． | 23° |
17．已知四边形ABCD是平行四边形，下列结论中不正确的是（ ）
| A． | 当AB=BC时，四边形ABCD是菱形 | B． | 当AC=BD时，四边形是正方形 | ||
| C． | 当∠ABC=90°时，四边形是矩形 | D． | 当AC⊥BD时，四边形是菱形 |