题目内容
(1)等式
=a+2成立的条件是什么?
(2)当x 时,代数式
有意义;
(3)当x 时,代数式
有意义;
(4)当x 时,代数式
无意义.
| (a+2)2 |
(2)当x
| 1-2x |
(3)当x
| x2+1 |
(4)当x
| x-1 |
考点:二次根式的性质与化简,二次根式有意义的条件
专题:
分析:(1)根据二次根式的性质:
=a (a≥0),可得答案;
(2)根据被开方数是非负数,可得答案;
(3)根据被开方数是非负数,可得答案;
(4)根据被开方数是非负数,可得答案.
| a2 |
(2)根据被开方数是非负数,可得答案;
(3)根据被开方数是非负数,可得答案;
(4)根据被开方数是非负数,可得答案.
解答:解:(1)由等式
=a+2成立,得
a+2≥0.解得a≥-2,
当a≥-2时,等式
=a+2成立;
(2)要使代数式
有意义,得
1-2x≥0,解得x≤
.
当x≤
时,代数式
有意义;
(3)由x2+1≥1得
x为任意实数,代数式
有意义;
(3)要使代数式
无意义,得
x-1<0,解得x<1.
当x<1时,代数式
无意义;
故答案为:≤
,任意实数,≤1.
| (a+2)2 |
a+2≥0.解得a≥-2,
当a≥-2时,等式
| (a+2)2 |
(2)要使代数式
| 1-2x |
1-2x≥0,解得x≤
| 1 |
| 2 |
当x≤
| 1 |
| 2 |
| 1-2x |
(3)由x2+1≥1得
x为任意实数,代数式
| x2+1 |
(3)要使代数式
| x-1 |
x-1<0,解得x<1.
当x<1时,代数式
| x-1 |
故答案为:≤
| 1 |
| 2 |
点评:本题考查了二次根式有意义的条件,利用二次根式的被开方数是非负数得出不等是解题关键.

练习册系列答案
相关题目
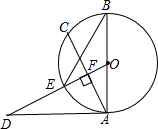 如图所示,⊙O直径AB=10,AD是⊙O的切线,OD⊥弦AC于点F,且交⊙O于点E,有下列结论:
如图所示,⊙O直径AB=10,AD是⊙O的切线,OD⊥弦AC于点F,且交⊙O于点E,有下列结论: 在△ABC中,AB=AC,∠BAC<90°,CD、BE分别为△ABC的中线,AF⊥CD,AG⊥BE,分别交CD、BE的延长线于点F、G,试问:
在△ABC中,AB=AC,∠BAC<90°,CD、BE分别为△ABC的中线,AF⊥CD,AG⊥BE,分别交CD、BE的延长线于点F、G,试问: