ЬтФПФкШн
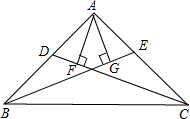
 дкЁїABCжаЃЌAB=ACЃЌЁЯBACЃМ90ЁуЃЌCDЁЂBEЗжБ№ЮЊЁїABCЕФжаЯпЃЌAFЁЭCDЃЌAGЁЭBEЃЌЗжБ№НЛCDЁЂBEЕФбгГЄЯпгкЕуFЁЂGЃЌЪдЮЪЃК
дкЁїABCжаЃЌAB=ACЃЌЁЯBACЃМ90ЁуЃЌCDЁЂBEЗжБ№ЮЊЁїABCЕФжаЯпЃЌAFЁЭCDЃЌAGЁЭBEЃЌЗжБ№НЛCDЁЂBEЕФбгГЄЯпгкЕуFЁЂGЃЌЪдЮЪЃКЃЈ1ЃЉAFгыAGЯрЕШТ№ЃПЮЊЪВУДЃП
ЃЈ2ЃЉЕБЁЯBAC=90ЁуЪБЃЌЦфгрЬѕМўВЛБфЃЌВТЯыAF
ЃЈ3ЃЉЕБЁЯBACЃО90ЁуЪБЃЌЦфгрЬѕМўВЛБфЃЌВТЯыAF
ЃЈ4ЃЉЭЈЙ§БОЬтЃЌФуПЩвдЕУЕННсТлЃКЕШбќШ§НЧаЮЕФЖЅЕуЕНСНбќжаЯпЫљдкжБЯпЕФОрРы
ПМЕуЃКШЋЕШШ§НЧаЮЕФХаЖЈгыаджЪ,ЕШбќШ§НЧаЮЕФаджЪ
зЈЬтЃК
ЗжЮіЃКЃЈ1ЃЉЧѓГіAD=AEЃЌИљОнSASЭЦГіЁїABEЁеЁїACDЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУГіЁЯABG=ЁЯACFЃЌЧѓГіЁЯAGB=ЁЯAFCЃЌИљОнASAЭЦГіЁїAGBЁеЁїAFCМДПЩЃЛ
ЃЈ2ЃЉЧѓГіAD=AEЃЌИљОнSASЭЦГіЁїABEЁеЁїACDЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУГіЁЯABG=ЁЯACFЃЌЧѓГіЁЯAGB=ЁЯAFCЃЌИљОнASAЭЦГіЁїAGBЁеЁїAFCМДПЩЃЛ
ЃЈ3ЃЉЧѓГіAD=AEЃЌИљОнSASЭЦГіЁїABEЁеЁїACDЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУГіЁЯABG=ЁЯACFЃЌЧѓГіЁЯAGB=ЁЯAFCЃЌИљОнASAЭЦГіЁїAGBЁеЁїAFCМДПЩЃЛ
ЃЈ4ЃЉИљОнвдЩЯНсТлЕУГіМДПЩЃЎ
ЃЈ2ЃЉЧѓГіAD=AEЃЌИљОнSASЭЦГіЁїABEЁеЁїACDЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУГіЁЯABG=ЁЯACFЃЌЧѓГіЁЯAGB=ЁЯAFCЃЌИљОнASAЭЦГіЁїAGBЁеЁїAFCМДПЩЃЛ
ЃЈ3ЃЉЧѓГіAD=AEЃЌИљОнSASЭЦГіЁїABEЁеЁїACDЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУГіЁЯABG=ЁЯACFЃЌЧѓГіЁЯAGB=ЁЯAFCЃЌИљОнASAЭЦГіЁїAGBЁеЁїAFCМДПЩЃЛ
ЃЈ4ЃЉИљОнвдЩЯНсТлЕУГіМДПЩЃЎ
НтД№ЃКНтЃКЃЈ1ЃЉAF=AGЃЌ
РэгЩЪЧЃКЁпCDКЭBEЪЧЁїABCЕФжаЯпЃЌ
ЁрAE=
ACЃЌAD=
ABЃЌ
ЁпAC=ABЃЌ
ЁрAD=AEЃЌ
дкЁїABEКЭЁїACDжа
ЁрЁїABEЁеЁїACDЃЈSASЃЉЃЌ
ЁрЁЯABG=ЁЯACFЃЌ
ЁпAFЁЭCDЃЌAGЁЭBEЃЌ
ЁрЁЯAGB=ЁЯAFCЃЌ
дкЁїAGBКЭЁїAFCжа
ЁрЁїAGBЁеЁїAFCЃЈASAЃЉЃЌ
ЁрAF=AGЃЛ
ЃЈ2ЃЉAF=AGЃЌ
РэгЩЪЧЃКЁпCDКЭBEЪЧЁїABCЕФжаЯпЃЌ
ЁрAE=
ACЃЌAD=
ABЃЌ
ЁпAC=ABЃЌ
ЁрAD=AEЃЌ
дкЁїABEКЭЁїACDжа
ЁрЁїABEЁеЁїACDЃЈSASЃЉЃЌ
ЁрЁЯABG=ЁЯACFЃЌ
ЁпAFЁЭCDЃЌAGЁЭBEЃЌ
ЁрЁЯAGB=ЁЯAFCЃЌ
дкЁїAGBКЭЁїAFCжа
ЁрЁїAGBЁеЁїAFCЃЈASAЃЉЃЌ
ЁрAF=AGЃЌ
ЙЪД№АИЮЊЃК=ЃЛ
ЃЈ3ЃЉAF=AGЃЌ
РэгЩЪЧЃКЁпCDКЭBEЪЧЁїABCЕФжаЯпЃЌ
ЁрAE=
ACЃЌAD=
ABЃЌ
ЁпAC=ABЃЌ
ЁрAD=AEЃЌ
дкЁїABEКЭЁїACDжа
ЁрЁїABEЁеЁїACDЃЈSASЃЉЃЌ
ЁрЁЯABG=ЁЯACFЃЌ
ЁпAFЁЭCDЃЌAGЁЭBEЃЌ
ЁрЁЯAGB=ЁЯAFCЃЌ
дкЁїAGBКЭЁїAFCжа
ЁрЁїAGBЁеЁїAFCЃЈASAЃЉЃЌ
ЁрAF=AGЃЌ
ЙЪД№АИЮЊЃК=ЃЛ
ЃЈ4ЃЉЭЈЙ§БОЬтЃЌФуПЩвдЕУЕННсТлЃКЕШбќШ§НЧаЮЕФЖЅЕуЕНСНбќжаЯпЫљдкжБЯпЕФОрРыЯрЕШЃЌ
ЙЪД№АИЮЊЃКЯрЕШЃЎ
РэгЩЪЧЃКЁпCDКЭBEЪЧЁїABCЕФжаЯпЃЌ
ЁрAE=
| 1 |
| 2 |
| 1 |
| 2 |
ЁпAC=ABЃЌ
ЁрAD=AEЃЌ
дкЁїABEКЭЁїACDжа
|
ЁрЁїABEЁеЁїACDЃЈSASЃЉЃЌ
ЁрЁЯABG=ЁЯACFЃЌ
ЁпAFЁЭCDЃЌAGЁЭBEЃЌ
ЁрЁЯAGB=ЁЯAFCЃЌ
дкЁїAGBКЭЁїAFCжа
|
ЁрЁїAGBЁеЁїAFCЃЈASAЃЉЃЌ
ЁрAF=AGЃЛ

ЃЈ2ЃЉAF=AGЃЌ
РэгЩЪЧЃКЁпCDКЭBEЪЧЁїABCЕФжаЯпЃЌ
ЁрAE=
| 1 |
| 2 |
| 1 |
| 2 |
ЁпAC=ABЃЌ
ЁрAD=AEЃЌ
дкЁїABEКЭЁїACDжа
|
ЁрЁїABEЁеЁїACDЃЈSASЃЉЃЌ
ЁрЁЯABG=ЁЯACFЃЌ
ЁпAFЁЭCDЃЌAGЁЭBEЃЌ
ЁрЁЯAGB=ЁЯAFCЃЌ
дкЁїAGBКЭЁїAFCжа
|
ЁрЁїAGBЁеЁїAFCЃЈASAЃЉЃЌ
ЁрAF=AGЃЌ
ЙЪД№АИЮЊЃК=ЃЛ
ЃЈ3ЃЉAF=AGЃЌ

РэгЩЪЧЃКЁпCDКЭBEЪЧЁїABCЕФжаЯпЃЌ
ЁрAE=
| 1 |
| 2 |
| 1 |
| 2 |
ЁпAC=ABЃЌ
ЁрAD=AEЃЌ
дкЁїABEКЭЁїACDжа
|
ЁрЁїABEЁеЁїACDЃЈSASЃЉЃЌ
ЁрЁЯABG=ЁЯACFЃЌ
ЁпAFЁЭCDЃЌAGЁЭBEЃЌ
ЁрЁЯAGB=ЁЯAFCЃЌ
дкЁїAGBКЭЁїAFCжа
|
ЁрЁїAGBЁеЁїAFCЃЈASAЃЉЃЌ
ЁрAF=AGЃЌ
ЙЪД№АИЮЊЃК=ЃЛ
ЃЈ4ЃЉЭЈЙ§БОЬтЃЌФуПЩвдЕУЕННсТлЃКЕШбќШ§НЧаЮЕФЖЅЕуЕНСНбќжаЯпЫљдкжБЯпЕФОрРыЯрЕШЃЌ
ЙЪД№АИЮЊЃКЯрЕШЃЎ
ЕуЦРЃКБОЬтПМВщСЫШЋЕШШ§НЧаЮЕФаджЪКЭХаЖЈЕФгІгУЃЌжївЊПМВщбЇЩњЕФЭЦРэФмСІЃЌжЄУїЙ§ГЬРрЫЦЃЌзЂвтЃКШЋЕШШ§НЧаЮЕФХаЖЈЖЈРэгаSASЃЌASAЃЌAASЃЌSSSЃЌШЋЕШШ§НЧаЮЕФЖдгІБпЯрЕШЃЌЖдгІНЧЯрЕШЃЎ

СЗЯАВсЯЕСаД№АИ
ЯрЙиЬтФП
ЯТСагяОфе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
AЁЂ-
| ||||
BЁЂ-
| ||||
CЁЂ-
| ||||
DЁЂ
|
ЯТУцдЫЫуе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
| AЁЂ3ab+3ac=3abc |
| BЁЂ4a2b-4b2a=0 |
| CЁЂ2x2+7x2=9x4 |
| DЁЂ3y2-2y2=y2 |
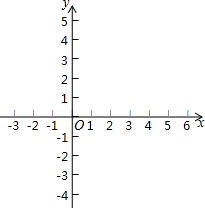 вбжЊЖўДЮКЏЪ§ЕФЭМЯѓЕФЖдГЦжсЪЧжБЯпx=1ЃЌЫќгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгыЕуCЃЌЕуAЁЂCЕФзјБъЗжБ№ЪЧЃЈ-1ЃЌ0ЃЉЁЂЃЈ0ЃЌ
вбжЊЖўДЮКЏЪ§ЕФЭМЯѓЕФЖдГЦжсЪЧжБЯпx=1ЃЌЫќгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгыЕуCЃЌЕуAЁЂCЕФзјБъЗжБ№ЪЧЃЈ-1ЃЌ0ЃЉЁЂЃЈ0ЃЌ ШчЭМЃЌвбжЊЯпЖЮAB=CDЃЌЧвЫќУЧБЫДЫжиКЯИїздЕФ
ШчЭМЃЌвбжЊЯпЖЮAB=CDЃЌЧвЫќУЧБЫДЫжиКЯИїздЕФ