题目内容
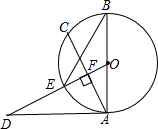 如图所示,⊙O直径AB=10,AD是⊙O的切线,OD⊥弦AC于点F,且交⊙O于点E,有下列结论:
如图所示,⊙O直径AB=10,AD是⊙O的切线,OD⊥弦AC于点F,且交⊙O于点E,有下列结论:(1)AD=AC;
(2)∠DAC=2∠OEB;
(3)当AC=BE时,DE=5;
则其中正确的是
考点:切线的性质
专题:
分析:证明OA⊥DA,AC⊥OD,得到∠D+∠DAF=∠FOA+∠D,进而得到∠DAF=∠FOA;证明∠OBE=∠OEB,进而得到∠FOA=2∠OEB,问题即可解决.
解答: 解:∵AD是⊙O的切线,
解:∵AD是⊙O的切线,
∴OA⊥DA;而AC⊥OD,
∴∠D+∠DAF=∠FOA+∠D,
∴∠DAF=∠FOA;
∵OB=OE,
∴∠OBE=∠OEB,
∴∠FOA=2∠OEB,
∴∠DAC=2∠OEB.
故正确答案为(2).
 解:∵AD是⊙O的切线,
解:∵AD是⊙O的切线,∴OA⊥DA;而AC⊥OD,
∴∠D+∠DAF=∠FOA+∠D,
∴∠DAF=∠FOA;
∵OB=OE,
∴∠OBE=∠OEB,
∴∠FOA=2∠OEB,
∴∠DAC=2∠OEB.
故正确答案为(2).
点评:该题主要考查了圆的切线的性质及其应用问题;解题的关键是借助切线的性质灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
下列语句正确的是( )
A、-
| ||||
B、-
| ||||
C、-
| ||||
D、
|
 如图,?ABCD中,点E是BC的中点.
如图,?ABCD中,点E是BC的中点. 如图,直线l经过点B(0,2),与x轴的正半轴交于点A,△ABO的面积为3,求直线l的函数表达式.
如图,直线l经过点B(0,2),与x轴的正半轴交于点A,△ABO的面积为3,求直线l的函数表达式. 已知二次函数的图象的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交与点C,点A、C的坐标分别是(-1,0)、(0,
已知二次函数的图象的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交与点C,点A、C的坐标分别是(-1,0)、(0,