题目内容
已知线段AB=m,在直线AB上取一点P,恰好是AP:PB=n:1,点Q为PB的中点,求线段AQ的长.
考点:两点间的距离
专题:
分析:由于点P的位置不能确定,故应分点P在线段AB上时,先根据比值求出AP,PB的长度,再根据中点定义求出PQ的长度,相加即可求出AQ的长度;当点P在线段AB的延长线上时,根据比值求出BP的长度,再根据中点定义求出BQ的长度,相加即可求出AQ的长度.
解答:解:如图1,点P在线段AB上时,
∵AB=m,AP:PB=n:1,
∴AP=
,PB=
,
∵点Q为PB的中点,
∴PQ=
PB=
,
∴AQ=AP+PQ=
+
=
;
如图2,点P在线段AB的延长线上时,
∵AB=m,AP:PB=n:1,
∴
=
,
解得BP=
,
∵点Q为PB的中点,
∴BQ=
BP=
,
∴AQ=AB+BQ=m+
=
,
综上,线段AQ的长为
或
.

∵AB=m,AP:PB=n:1,
∴AP=
| mn |
| n+1 |
| m |
| m+n |
∵点Q为PB的中点,
∴PQ=
| 1 |
| 2 |
| m |
| 2(n+1) |
∴AQ=AP+PQ=
| mn |
| n+1 |
| m |
| 2(n+1) |
| m(2n+1) |
| 2(n+1) |
如图2,点P在线段AB的延长线上时,
∵AB=m,AP:PB=n:1,
∴
| m+BP |
| BP |
| n |
| 1 |
解得BP=
| m |
| n-1 |
∵点Q为PB的中点,
∴BQ=
| 1 |
| 2 |
| m |
| 2(n-1) |
∴AQ=AB+BQ=m+
| m |
| 2(n-1) |
| m(2n-1) |
| 2(n-1) |
综上,线段AQ的长为
| m(2n+1) |
| 2(n+1) |
| m(2n-1) |
| 2(n-1) |
点评:本题考查的是两点间的距离,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
下面运算正确的是( )
| A、3ab+3ac=3abc |
| B、4a2b-4b2a=0 |
| C、2x2+7x2=9x4 |
| D、3y2-2y2=y2 |
 已知二次函数的图象的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交与点C,点A、C的坐标分别是(-1,0)、(0,
已知二次函数的图象的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交与点C,点A、C的坐标分别是(-1,0)、(0,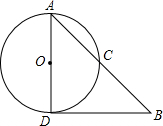 如图,AD为⊙O的直径,DE切⊙O于D,AE交⊙O于C,求证:AD2=AC•AE.
如图,AD为⊙O的直径,DE切⊙O于D,AE交⊙O于C,求证:AD2=AC•AE. 如图,已知线段AB=CD,且它们彼此重合各自的
如图,已知线段AB=CD,且它们彼此重合各自的