题目内容
5. 如图,己知AB是半径为2的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形.
如图,己知AB是半径为2的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形.(1)求证:△DFB是等腰三角形;
(2)若AF=1,求DA的长度;
(3)若DA=$\sqrt{7}$AF,求证:CF⊥AB.
分析 (1)由AB是⊙O直径,得到∠ACB=90°,由于△AEF为等边三角形,得到∠CAB=∠EFA=60°,根据三角形的外角的性质即可得到结论;
(2)根据等边三角形求出FM、AM、根据勾股定理求出AF即可;
(3)过点A作AM⊥DF于点M,设AF=2a,根据等边三角形的性质得到FM=EM=a,AM=$\sqrt{3}$a,在根据已知条件得到AB=AF+BF=8a,根据直角三角形的性质得到AE=EF=AF=CE=2a,推出∠ECF=∠EFC,根据三角形的内角和即可得到结论.
解答 (1)证明:∵AB是⊙O直径,
∴∠ACB=90°,
∵△AEF为等边三角形,
∴∠CAB=∠EFA=60°
∴∠B=30°,
∵∠EFA=∠B+∠FDB,
∴∠B=∠FDB=30°,
∴△DFB是等腰三角形;
(2)解:过点A作AM⊥DF于点M,
∵AB=2×2=4,AF=1,
∴BF=4-1=3,
∵DF=BF,
∴DF=3,
∵△AEF是等边三角形,
∴FM=EM=$\frac{1}{2}$AF=$\frac{1}{2}$,AM=$\sqrt{3}$FM=$\frac{\sqrt{3}}{2}$,
在Rt△DAM中,AD=$\sqrt{7}$AF=$\sqrt{7}$×1=$\sqrt{7}$;
(3)证明:设AF=2a,
∵△AEF是等边三角形,
∴FM=EM=a,AM=$\sqrt{3}$a,
在Rt△DAM中,AD=$\sqrt{7}$AF=2$\sqrt{7}$a,AM=$\sqrt{3}$a,
∴DM=5a,∴DF=BF=6a,
∴AB=AF+BF=8a,
在Rt△ABC中,∠B=30°,∠ACB=90°,
∴AC=4a,
∵AE=EF=AF=2a,
∴CE=AC-AE=2a,
∴∠ECF=∠EFC,
∵∠AEF=∠ECF+∠EFC=60°,
∴∠CFE=30°,
∴∠AFC=∠AFE+∠EFC=60°+30°=90°,
∴CF⊥AB.
点评 本题考查了圆周角定理,等边三角形的性质,等腰三角形的判定和性质,含30°角的直角三角形,勾股定理,正确的作出辅助线是解题的关键.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案| A. | 旭日东升 | B. | 潮起潮落 | C. | 瓮中捉鳖 | D. | 守株待兔 |
| A. | 锐角 | B. | 直角 | ||
| C. | 钝角 | D. | 以上三种都有可能 |
| A. | y=(x-1)2+2 | B. | y=(x+1)2+2 | C. | y=(x+3)2+2 | D. | y=(x-3)2+2 |
| A. | 在2.3到2.4之间 | B. | 在2.4到2.5之间 | C. | 在2.5到2.6之间 | D. | 在2.6到2.7之间 |
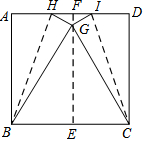 如图,将正方形ABCD对折,使点A点与D重合,点B与C重合,折痕EF;展开后再次折叠,使点A与点D重合于正方形内点G处,折痕分别为BH,CI,如果正方形ABCD的边长是2,则下列结论:①△GBC是等边三角形;②△IGH的面积是7$\sqrt{3}$-12;③tan∠BHA=2+$\sqrt{3}$;④GE=2$\sqrt{3}$,其中正确的个数有( )
如图,将正方形ABCD对折,使点A点与D重合,点B与C重合,折痕EF;展开后再次折叠,使点A与点D重合于正方形内点G处,折痕分别为BH,CI,如果正方形ABCD的边长是2,则下列结论:①△GBC是等边三角形;②△IGH的面积是7$\sqrt{3}$-12;③tan∠BHA=2+$\sqrt{3}$;④GE=2$\sqrt{3}$,其中正确的个数有( )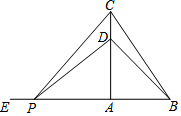 如图,在△ABC中,∠BAC=90°,AB=3 cm,BC=5 cm,点D在线段AC上,且CD=1 cm,动点P从BA的延长线上距A点5 cm的E点出发,以每秒2 cm的速度沿射线EA的方向运动了t秒.
如图,在△ABC中,∠BAC=90°,AB=3 cm,BC=5 cm,点D在线段AC上,且CD=1 cm,动点P从BA的延长线上距A点5 cm的E点出发,以每秒2 cm的速度沿射线EA的方向运动了t秒.